La presente investigación se desarrolló en el marco de la educación no presencial por las condiciones sanitarias que actualmente se vive debido al COVID-19 en la Universidad Nacional Intercultural “Fabiola Salazar Leguía” de Bagua, en la carrera profesional de Ingeniería Civil, cuya estructura silábica del curso de Métodos Numéricos permite desarrollar actividades experimentales relacionadas a la simulación numérica y gráfica. Esta experiencia surge desde la necesidad de establecer aprendizajes significativos, el objetivo que persigue esta indagación es aplicar el método de Montecarlo para resolver un problema concreto de geometría que consiste en determinar el volumen de la pulpa de cocos, resaltando que en la provincia de Bagua y zonas aledañas se produce significativamente el coco, y es menester conocer su volumen para efectos de comercialización de su pulpa y posterior extracción de aceites. El algoritmo planteado permitiría estimar de manera muy cercana el volumen de la pulpa de un coco sin necesidad de seccionarlo, a través de este método se establece en promedio un margen de error porcentual por debajo del 9% del volumen real medido respecto al resultado de la simulación en el lenguaje de programación Basic. El método Montecarlo utilizado como estrategia de enseñanza resulta muy útil pues propicia aprendizajes significativos en un ambiente lúdico, así como propicia el uso de materiales de su comunidad.

Palabras claves: simulación, números aleatorios, Montecarlo, coco.

ABSTRACT

This research was developed within the framework of non-face-to-face education due to the sanitary conditions that currently exist due to COVID-19 at the “Fabiola Salazar Leguía” National Intercultural University of Bagua, in the professional career of Civil Engineering, whose syllabic structure The course of Numerical Methods allows to develop experimental activities related to numerical and graphic simulation. This experience arises from the need to establish significant learning, the objective pursued by this investigation is to apply the Monte Carlo method to solve a specific geometry problem that consists of determining the volume of coconut pulp, highlighting that in the province of Bagua and Coconut is produced significantly in neighboring areas, and it is necessary to know its volume for the purposes of marketing its pulp and subsequent extraction of oils. The proposed algorithm would allow to estimate very closely the volume of the pulp of a coconut without having to section it, through this method a margin of percentage error is established on average below 9% of the real volume measured with respect to the result of the simulation in the Basic programming language. The Monte Carlo method used as a teaching strategy is very useful as it fosters meaningful learning in a playful environment, as well as the use of materials from its community.

Keywords: simulation, random numbers, Monte Carlo, coco.

INTRODUCCIÓN

La estrategia de trabajo virtual en el semestre 2020-I ha representado un desafío para los docentes en general, y para nuestra universidad en particular, pues la no presencialidad propició en más frecuencia que lo acostumbrado que la parte experimental quede relegada o circunscrita a reproducciones domiciliarias o de su entorno más cercano con la finalidad de evitar el contacto o la coincidencia de varios estudiantes en espacios reducidos.

En este sentido, el curso de métodos numéricos de la carrera de ingeniería civil representó un espacio de trabajo virtual muy instructivo para poner en práctica tanto el rigor matemático como el manejo de un lenguaje de programación orientado a resolver problemas concretos relacionados a elementos de su entorno y cultura.

El coco: un producto aprovechable

Figura 1

El coco “cocos nucifera”

Figura 2

El coco y su pulpa

Una de las especies vegetales que abunda de manera natural en la ciudad de Bagua- Amazonas- Perú es el cocos nucifera “coco”, cuyo consumo masivo de este producto se centra en su agua que alberga en su interior, y que es bien demandada en esta zona tropical, sin embargo en otras localidades del Perú el interés de este vegetal tropical gira en torno al aceite que se puede extraer de él, por ello es de suma importancia saber cuánta pulpa (copra) pueda tener en su interior el coco.

El método Montecarlo: muestreo artificial

También llamado simulación de Montecarlo o método de Montecarlo su origen se atribuye a los investigadores Stanislaw Ulam y John von Neumann por la década de 1940. Ambos sentaron las bases del método cuando participaban en el proyecto de investigación de la bomba atómica durante la II Guerra Mundial. La denominación de “Montecarlo” proviene de Mónaco, conocida como la capital del juego del azar, esto debido a que el juego de la ruleta era considerado como el primer generador de números aleatorios. La definición elemental de este método parte de la probabilidad, debido a que establece conocer la posibilidad de ocurrencia de un suceso o evento, que resulta realizando el experimento un número suficiente de veces y determinando la variable aleatoria dependiente (González, 2015).

El método Montecarlo representa una estrategia para la indagación y programación; esencialmente es una técnica de sondeo artificial, utilizada para operar de manera numérica sistemas grandes o complejos que posean componentes aleatorios, en otras palabras, es una técnica que fusiona conceptos estadísticos con la facilidad que poseen los sistemas informáticos para generar números pseudo-aleatorios y automatizar cálculos (Paisan & Moret, 2008).

Derivados del coco: prometedora actividad económica

Tabla 1

Producción de coco por departamentos (Toneladas)

Departamento	Producción
San Martín	14,476.00
Loreto	8,742.00
Ucayali	4,811.00
Piura	1,537.00
Huánuco	1,402.00
Junín	415.00
Madre de Dios	390.00
Ayacucho	143.00
Tumbes	140.00
Cajamarca	90.00
Lambayeque	54.00

Fuente: Ministerio de Agricultura y Riego, MINAGRI.(2014).

El fruto de un cocotero puede contener en promedio 300 ml de agua de coco, así mismo puede tener 2.5 kg de masa aproximadamente y puede medir unos 30 cm de perímetro, posee un aroma fresco tropical, posee propiedades que contribuyen a una buena salud por contener niveles altos de hierro y potasio. Además, su uso no se restringe a la bebida sino a la gastronomía e industria cosmética, etc. (Noli & Chamorro, 2019). La manteca de coco o también llamado aceite de coco, representa un tipo de aceite vegetal. El procedimiento para extraerlo es necesario ejercer presión mecánica sobre la pulpa del coco, y como consecuencia resulta un líquido que contiene un 90% de ácidos grasos. Este alto porcentaje graso hace posible que desacelere su proceso de oxidación por lo que puede mantenerse hasta medio año sin requerir refrigeración. Esta característica convierte al coco en un producto muy útil para la salud y belleza (Medina & Nina, 2019).

Otro derivado prometedor sería la cáscara del coco, que se utiliza como maceta ecológica o biodegradables, contribuyendo a la sostenibilidad del medioambiente, en reemplazo de las macetas de material plástico. (Nuñez, 2010).

El objetivo que persigue la presente indagación es aplicar el método de Montecarlo para resolver un problema concreto de geometría que consiste en determinar el volumen de la pulpa de coco. Asimismo, resaltar y valorar la utilidad de este fruto, tan abundante en la provincia de Bagua y zonas aledañas, por ello es importante aplicar este método que permitiría contribuir a la comercialización de su pulpa, así como la posterior extracción de aceites.

METODOLOGÍA

La educación virtual universitaria, así como la educación en general se basa en la pertinencia de los contenidos temáticos, de tal forma que para lograr aprendizajes significativos es necesario contextualizar la temática de cada curso, de esta forma surgió la idea de utilizar un producto bastante popular en esta zona tropical como es el coco.

La investigación se realizó con los estudiantes de ingeniería civil del V ciclo de la Universidad Nacional Intercultural “Fabiola Salazar Leguía” de Bagua-Amazona-Perú, en el curso de métodos numéricos. Ambos modelos matemáticos fueron desarrollados en clase a través de sesiones virtuales aplicando el método de Montecarlo dentro de las simulaciones numéricas, posteriormente se llevó a cabo un taller de capacitación para dotar de herramientas tecnológicas e informática a los estudiantes en programación Basic y métodos de simulación, desarrollándose múltiples casos de la aplicación del método aleatorio.

Figura 3

Proceso para obtener el volumen real de la pulpa de coco

Modelo matemático: el volumen del coco y su pulpa

Nuestro primer modelo matemático consideró al coco semejante a un cuerpo esférico, tal como indica la figura 2, donde los elementos geométricos que son necesarios estimar para un posterior cálculo del volumen de la pulpa, son el radio exterior ( e interior). Este último resultó de la simulación numérica aplicando el método Montecarlo, y con estos valores se calculó por fórmula el volumen del coco y volumen de la pulpa que contiene en su interior como lo evidencia la Tabla 2.

Tabla 2

Fórmulas para el cálculo del volumen del coco y su pulpa

Coco esférico

Coco elipsoide

Volumen del coco

Volumen de la pulpa del coco

Figura 2

Sección diametral del coco como esfera y elipsoide

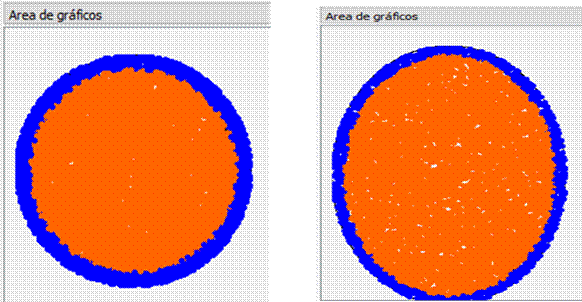
Para una estimación más aproximada a la realidad se trabajó con dos modelos matemáticos: el primero consideró al coco como una figura esférica donde era necesario medir el diámetro del coco para su posterior cálculo o simulación del volumen, y el segundo modelo consideró al coco como un elipsoide como muestra la figura 2. Aquí es menester medir el perímetro mayor y menor del coco lo que nos permitió determinar las longitudes de los tres ejes necesarios en un elipsoide, y luego se procedió al cálculo del volumen como indica la tabla 2.

Método Montecarlo: Proceso manual

Cada estudiante del curso seccionó o partió el coco y esparció de manera aleatoria pequeñas grajeas en cantidades conocidas sobre la pulpa del coco, para lo cual nos basaremos en el éxito, es decir que las grajeas que se ubican dentro de la zona de pulpa del coco y aquellas que caen en la zona central sumados corresponde al número total de grajeas. Posteriormente, los estudiantes del curso procedieron a realizar de manera manual, es decir contabilizando los elementos vertidos al azar, esto nos permitirá determinar la probabilidad y como consecuencia el radio interior

Método Montecarlo: Programación Basic

Un número elevado de veces que se realice los eventos garantiza mejor aproximación, esto representa una limitante cuando se realiza el proceso manual, por ello es más recomendable realizarlo por medio de un computador. Los estudiantes codificaron el algoritmo de simulación numérica teniendo en cuenta nuestro modelo matemático.

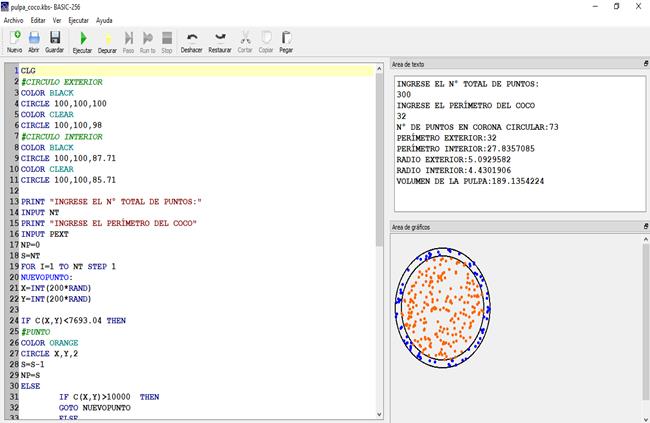
Figura 4

Programación Basic para estimación de volumen de la pulpa de coco

RESULTADOS

Se llevaron a cabo 28 mediciones realizadas por los estudiantes, de los cuales se obtuvo volúmenes promedio de pulpa de coco 160 cm³ hasta 600 cm³, evidenciándose que los perímetros registrados para esos volúmenes guardan una relación directa entre sí como se aprecia en la Tabla 3 y 4 y que se refleja en las figuras 5 y 6.

Tabla 3

Volumen real de la pulpa del coco, simulación numérica del coco esférico

Perimetro del coco(cm)	Volumen medido de pulpa de coco (cm³)	100 eventos Simulados Volumen(cm³)	1000 eventos simulados volumen(cm³)	10000 eventos Simulados volumen(cm³)
40	400	263	327	357
42.5	500	207	413	420
46	600	639	513	546
44	450	485	460	459
42	400	372	422	401
44	500	370	479	465
40.5	400	393	359	360
45.5	500	494	507	506
45.5	470	452	520	473
43	400	417	454	432
37	300	299	278	276
39	350	338	322	325
34	250	241	206	209
41	350	407	391	382
43	400	435	451	436
40	400	321	353	345
47	500	568	512	568
42	420	382	428	410
36	300	286	237	256
41.5	450	359	410	402
41	450	422	403	371
32	160	236	201	180
35	250	176	237	238
38	350	288	309	296
38.5	393	399	306	320
33.5	230	259	195	195
28.5	152	121	109	126
32	190	157	188	179

Se puede apreciar que para iguales o cercanos valores de perímetro del coco se obtienen distintos valores de volumen de pulpa, cuyo margen de incertidumbre es en promedio +/- 50 cm³ resultando en este intervalo valores aleatorios de volumen de pulpa.

Tabla 4

Volumen real de la pulpa del coco, simulación numérica del coco elipsoide

PERIMETRO DEL COCO	VOLUMEN MEDIDO DE PULPA DE COCO(cm³)	100 eventos Simulados Volumen(cm³)	1000 eventos Simulados Volumen(cm³)	10000 eventos Simulados Volumen(cm³	Perímetro mayor del coco(cm)	Perímetro menor del coco(cm)
40	400	337	360	369	40	39
42.5	500	498	449	438	42.5	41.5
46	600	553	578	563	46	45
44	450	370	411	412	44	43
42	400	382	434	416	42	41
44	500	507	458	482	44	43
40.5	400	350	384	365	40.5	39.5
45.5	500	554	536	535	45.5	44.5
45.5	470	688	533	508	45.5	44.5
43	400	446	441	449	37	36
37	300	298	268	288	37	36
39	350	365	326	330	39	38
34	250	216	220	219	34	33
41	350	401	392	378	41	40
43	400	472	438	447	43	42
40	400	336	346	360	40	39
47	500	587	614	552	47	46
42	420	462	417	414	42	41
36	300	255	253	263	36	35
41.5	450	351	408	394	41.5	40.5
41	450	405	405	389	41	40
32	160	191	184	179	32	31
35	250	261	241	240	35	34
38	350	294	309	313	38	37
38.5	393	268	332	321	38.5	37.5
33.5	230	205	209	211	33.5	32.5
28.5	152	116	124	129	28.5	27.5
32	190	144	196	183	32	31

Figura 5

Volúmenes medidos y simulados del coco-1° Modelo

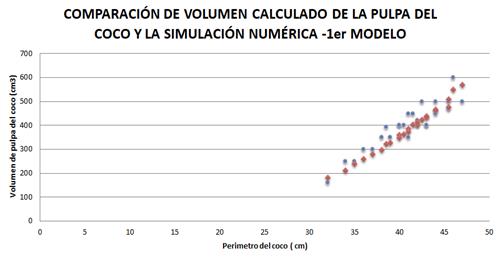
La simulación numérica del método Montecarlo se realizó teniendo en cuenta dos aproximaciones, el primer considerando al coco como una esfera obteniéndose mediante la simulación de Montecarlo volúmenes de pulpa más cercanos a los valores reales con un número de eventos aleatorios de 10000, lográndose valores más constantes con un error respecto al valor real en promedio de 10%.

Para la segunda aproximación de la simulación numérica del método Montecarlo, es decir considerando al coco como un elipsoide, se obtuvo volúmenes de pulpa mucho más cercanos a los valores reales con un número de eventos aleatorios de 10000, lográndose valores más constantes con un error respecto al valor real en promedio de 9%.

Figura 6

Volúmenes medidos y simulados del coco-2° Modelo

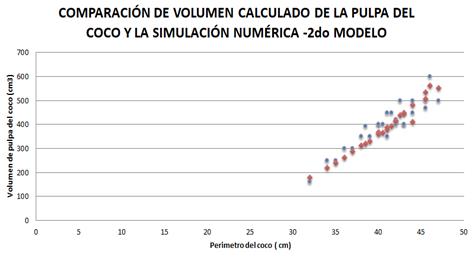
DISCUSIÓN

La simulación numérica por el método de Montecarlo nos permite estimar los valores de una determinada variable, teniendo en cuenta la aleatoriedad de esta; así mismo lo versátil de este método que basándose en la probabilidad de éxito o fracaso nos permite estimar con muy buena aproximación superficies como aplicación a la geometría (Garrido & Conesa, 2009).

El ordenador se constituye hoy por hoy en el laboratorio de los métodos numéricos, de la misma forma el método Montecarlo no solo se circunscribe a las aplicaciones puramente geométricas, sino también se podrían analizar procesos físicos o aplicativos como es el caso de la ingeniería, así como otros quehaceres académicos (Navone & Scancich, 2013).

Los valores estimados de las variables simuladas por el método Montecarlo tendrán mucho más margen de error respecto al valor real cuanto más pequeños sean los eventos aleatorios realizados en el ordenador, esto quiere decir que las variables adoptan sus valores “casi constantes” en la medida que aumentemos el número de sucesos o eventos al azar para que los resultados sean los más confiables (Marinilli, 2009).

Los resultados en las estimaciones usando el método Montecarlo dependerán mucho también del modelo matemático planteado. Además, es muy importante seleccionar adecuadamente el método numérico para generar mejor eficacia en nuestras aproximaciones (Murrugarra, 2014).

La modelación de Montecarlo nos ofrece una ventaja adicional frente a la indagación en laboratorio, dado que este procedimiento no necesita manipular físicamente los elementos a estudiar, donde la simulación numérica o gráfica resulta de menos costo que la puesta en marcha de una experimentación en la vida real. Otros beneficios se relacionan con la facilidad de monitorear el desenvolvimiento de los sistemas en modelación frente a sucesos variables de experimentación, de esta forma se comprende sus procesos internos y analizan los patrones de la evolución de estos modelos permitiendo predecir los entornos variables de la vida real (Prieto & Cabrera, 2020).

CONCLUSIONES

El mayor número de eventos aleatorios realizado en los programas de la simulación numérica de Montecarlo permite que los volúmenes de la pulpa de coco sean los más cercanos a los valores reales medidos por los estudiantes.

Los dos modelos matemáticos para el coco, como figura geométrica esférica y elipsoide, permiten estimar valores de volúmenes de pulpa de coco mucho más cercanos a los valores reales.

Las cantidades o el volumen de pulpa de coco, que se obtienen en la simulación numérica por el método de Montecarlo para una medición del perímetro, resulta un valor aleatorio dentro de un determinado intervalo.

El uso del método Montecarlo dentro de la simulación numérica en el curso de métodos numéricos representó una estrategia muy útil, ya que generó aprendizajes significativos creando espacios virtuales lúdicos.

REFERENCIAS BIBLIOGRÁFICAS

Barbat, A. H., Vargas, Y. F., Pujades, L. G., & Hurtado, J. E. (2016). Evaluación probabilista del riesgo sísmico de estructuras con base en la degradación de rigidez. Revista Internacional de Métodos Numéricos Para Cálculo y Diseño En Ingeniería, 32(1), 39–47. https://doi.org/10.1016/j.rimni.2014.11.001

Bueno, F., & Manzano, D. (2013). Técnicas Monte Carlo para la enseñanza de la estadística. In Actas de las Jornadas Virtuales en Didáctica de la Estadística, Probabilidad y Combinatoria (pp. 579–585). Granada.

Caballero, R. (2017). Monte Carlo - Metropolis Investigations of Shape and Matrix Effects in 2D and 3D Spin-Crossover Nanoparticles (pp. 1–31). Pontificia Universidad Católica del Perú.

De La Espriella, N., Casiano, G., & Ortega, C. (2012). Efecto de los Campos Cristalinos en un Ferromagneto de Ising Mixto Bidimensional. Información Tecnológica, 23(5), 125–134. https://doi.org/10.4067/S0718-07642012000500013

Garrido, A., & Conesa, E. (2009). Simulación por el método de Monte Carlo para generar criterios de aceptación en el control de calidad de productos de construcción. Informes de La Construcción, 61, 77–85. https://doi.org/10.3989/ic.09.025

González, J. (2015). Introducción del Factor Humano al Análisis de Riesgo (pp. 1–2921). Universidad Politécnica de Catalunya.

Lopaczek, A. A., & Gerbaudo, G. M. (2018). Análisis estocástico de vulnerabilidad sísmica de un puente mediante simulación de montecarlo. Asociación Argentina de Mecánica Computacional, XXXVI, 6–9.

Losilla, J. (1994). Herramientas para un laboratorio de estadística fundamentado en técnicas Monte Carlo (pp. 1–163). Universidad Autónoma de Barcelona.

Marinilli, A. (2009). Análisis probabilístico simplificado de pórticos de concreto reforzado ante acciones sísmicas. Boletín Técnico Instituto de Materiales y Modelos Estructurales, 47(2), 27–36.

Márquez, J., & Aparicio, J. (2010). Un modelo Monte Carlo para la Cámara de Diputados en México. Política y Gobierno, 17(2), 351–379.

Medina, C., & Nina, N. (2019). Efectividad de uso del aceite de coco (Cocos Nucífera) en el tratamiento de la Gingivitis, en personas de 10 a 20 años de la localidad de Milpo - Pasco - Enero – Julio del 2018. Universidad Nacional Daniel Alcides Carrión.

MINAGRI. (2014). Ministerio de Agricultura y Riego. Recuperado de www.minagri.gob.pe

Montiel, B. M., Goddard, J., & De los Cobos, S. (2008). Simulación Monte Carlo para el juego Siete y medio. Contáctos, 13–22.

Muglia, J. (2011). Simulaciones computacionales del Modelo de Ising con gradiente térmico (pp. 1–42). Universidad Nacional de La Plata.

Murrugarra, F. C. (2014). El método de Monte Carlo y los desarrollos asintóticos. Anales Científicos, 75(2), 288–293.

Navone, H., & Scancich, M. (2013). Dados , palitos , pixels y bits : Alternativas didácticas para explorar la metodología de Monte Carlo en un tono lúdico. Revista de Matemática: Teoría y Aplicaciones, 20(2), 275–288.

Noli, A., & Chamorro, C. (2019). Estudio de prefactibilidad para la instalación de una planta productora de aceite de coco. Universidad de Lima.

Nuñez, R. (2010). Estudio tecnológico del componente fibra de dos variedades de coco enano ( cocos nucifera) de los distritos de Lamas, Tarapoto y Pucacaca en la Región San Martín. Universidad Nacional de San Martín.

Paisan, Y. P., & Moret, J. P. (2008). Determinación de la incertidumbre de medición por el método de Monte Carlo en los procesos de manufactura. Tecnología Química, 28(3), 56–62.

Peñafiel, V., & Andrade, M. (2013). Simulación Monte Carlo para registros de precipitación Pluvial. Revista Bolivariana De Física, 22(1), 21–28.

Pérez, L. (2016). Aplicaci’oon del método de Montecarlo al análisis de falla de placas laminadas, bajo carga puntual constante en su centro (pp. 1–59). Universidad Tecnológica de Bolívar.

Picón, E. (2004). Una comparación Monte Carlo de tres métodos métricos de segmentación con análisis conjunto. Psicológica, 25, 231–252.

Polo, I. O. (2014). Simulación del funcionamiento de una cámara gamma mediante método Monte Carlo. Revista de Física Médica, 15(1), 6–8.

Prieto, G., & Cabrera, D. (2020). Diseño y evaluación de una estrategia lúdica de aprendizaje para enseñar Simulación de Montecarlo. Espacios, 41(13).

Salazar, E., & Alzate, W. (2018). Aplicación de la simulación Monte Carlo en la proyección del estado de resultados. Un estudio de caso. Espacios, 39(51), 1–10.

Sánchez, O. (2015). Simulación Montecarlo aplicada a un problema de acarreo en el minado superficial. Revista Del Instituto de Investigación de Ingeniería de Minas - UNMSM, 18(36), 101–108.

Vanalle, R. M., Lucato, W. C., Vieira, M., & Sato, I. D. (2012). Uso de la Simulación Monte Carlo para la Toma de Decisiones en una Línea de Montaje de una Fábrica. Información Tecnológica, 23(4), 33–44. https://doi.org/10.4067/S0718-07642012000400005

Vergara, M., & Maya, Vc. (2009). Estimación del valor en riesgo en un portafolio accionario Structured Monte Carlo. ADMINISTER, 1(15), 68–88.

Zapata, C., Piñeros, L., & Castaño, D. (2004). El método de simulación de montecarlo en estudios de confiabilidad de sistemas de distribución de energía eléctrica. Scientia et Technica, X(24), 55–60.

[1] Universidad Nacional Intercultural "Fabiola Salazar Leguía" de Bagua. Facultad de Ingenierías. Carrera profesional de Ingeniería Civil.

^{^[2]} I.E Tupac Amaru de Chiriaco Coordinación Académica.