Veritas
Et Scientia
Vol. 10. N° 1
Enero - junio del 2021
ISSN Edición Online:
2617-0639
DOI: https://doi.org/10.47796/ves.v10i1.464
ARTÍCULO ORIGINAL
DISEÑO E IMPLEMENTACIÓN DE UNA RED
NEURONAL ARTIFICIAL PARA PREDECIR EL RENDIMIENTO ACADÉMICO EN ESTUDIANTES DE
INGENIERÍA CIVIL DE LA UNIFSLB
DESIGN AND IMPLEMENTATION OF AN ARTIFICIAL NEURAL
NETWORK TO PREDICT ACADEMIC PERFORMANCE IN CIVIL ENGINEERING STUDENTS FROM
UNIFSLB
Fernando
Alain Incio Flores[1]
![]() https://orcid.org/0000-0003-3286-7787
https://orcid.org/0000-0003-3286-7787
fincio@ucvvirtual.edu.pe
Dulce
Lucero Capuñay Sanchez1
![]() https://orcid.org/0000-0001-8678-5766
https://orcid.org/0000-0001-8678-5766
Ronald
Omar Estela Urbina[2]
![]() https://orcid.org/0000-0001-5240-1242
https://orcid.org/0000-0001-5240-1242
Jorge
Antonio Delgado Soto[3]
![]() https://orcid.org/0000-0003-2275-8608
https://orcid.org/0000-0003-2275-8608
Segundo
Edilberto Vergara Medrano[4]
![]() https://orcid.org/0000-0001-7611-3827
https://orcid.org/0000-0001-7611-3827
Aceptado: 20/03/2021
Publicado online:30/05/2021
![]()
RESUMEN
Predecir
los resultados académicos de los estudiantes permite al docente buscar técnicas
y estrategias en el tiempo indicado durante el proceso de enseñanza y
aprendizaje con el fin de mejorar el logro de competencias en sus estudiantes.
En esta investigación se implementó una red neuronal artificial (RNA) para
predecir los resultados académicos del curso de física de los estudiantes del
II ciclo de la carrera profesional de Ingeniería Civil de la universidad
Nacional Intercultural Fabiola Salazar Leguía de Bagua-Perú en función de datos
históricos. La RNA se diseñó e implemento en el Software MATLAB, su
arquitectura está formada por una capa de entrada, una capa oculta y una capa
de salida, para el entrenamiento de la RNA se utilizó dos algoritmos que posee
la Toolbox de MATLAB: el Scaled Conjugate Gradient logrando un porcentaje de
predicción del 70% y el Levenberg-Marquardt logrando un porcentaje de
predicción 86%.
Palabras clave: Rendimiento académico, red neuronal
artificial, predicción.
ABSTRACT
Predicting the
academic results of students allows the teacher to seek techniques and
strategies at the indicated time during the teaching and learning process in
order to improve the achievement of skills in their students. In this research,
an artificial neural network (ANN) was implemented to predict the academic
results of the physics course of the students of the II cycle of the Civil
Engineering career of the National Intercultural University Fabiola Salazar
Leguía de Bagua-Peru based on data historical. The RNA was designed and
implemented in the MATLAB Software, its architecture is made up of an input
layer, a hidden layer and an output layer, for the RNA training two algorithms
that the MATLAB Toolbox has: the Scaled Conjugate Gradient achieving a prediction
percentage of 70% and the Levenberg-Marquardt achieving a prediction percentage
of 86%.
Keywords: Academic performance, artificial neural network, prediction.
![]()
INTRODUCCIÓN
Las
redes neuronales artificiales a lo largo de los años se han convertido en
modelos efectivos de predicción, han demostrado mejor efectividad frente a
modelos estadísticos de regresión sin necesidad de cumplir condiciones de
linealidad, normalidad, tamaño muestral, entre otros (Aranda-Corral
et al., 2014; Samani et al., 2017). La Matemática es el sustento de
la Física, y la Física es el sustento de la ingeniería (Popenici y Kerr, 2017),
los datos proporcionados por la oficina de asuntos académicos de la Universidad
Nacional Intercultural Fabiola Salazar Leguía de Bagua (UNIFSLB) evidencian
cierto grado de dificultad de los estudiantes de Ingeniería Civil para el logro
de competencias en la asignatura de Física, evidentemente esto origina
preocupación puesto que la carrera profesional de Ingenería Civil tiene un
fundamento físico-matemático, en tal sentido surge la necesidad de implementar
modelos matemáticos computacionales que permitan predecir los resultados
académicos haciendo uso de los datos históricos con el objetivo de proporcionar
al docente información oportuna y a tiempo para que pueda hacer uso de diversas
técnicas y estrategias de aprendizaje a fin de mejorar estos posibles
resultados.
Una RNA es un modelo matemático computacional
formado por una capa de entrada, capas de salidas y capas ocultas, estás a su
vez están constituidas por neuronas artificiales e interconectadas mediante
sinapsis, cada sinapsis con su respectivo peso, el funcionamiento de una RNA se
asemeja al comportamiento del cerebro humano , capaz de aprender mediante el
aprendizaje, precedido de un entrenamiento repetitivo (Amershi et al.,
2005; Brazdil y Jorge, 2001; Brusilovsky y Peylo, 2003; Garrido, 2010; Vila y
Penín, 2007).
La educación universitaria en el siglo XXI se
ha caracterizado por fomentar el logro de competencias en los estudiantes, en
este sentido el rendimiento académico es la evaluación cuantitativa y
cualitativa del logro de competencias expresados finalmente en una escala
vigesimal en el sistema de evaluación de la UNIFSLB. El logro o no de las
competencias en los estudiantes está influenciado por diversos factores de
orden emocional, cognitivo y socio cultural (Cerda et al., 2019; Edel,
2003; Garbanzo, 2007; Pinto et al., 2020; Salanova et al., 2005)
quienes intervienen positivamente o negativamente en el rendimiento académico
de los estudiantes.
Las RNAs es una de las herramientas que ofrece
la inteligencia artificial (IA), muy potente y efectiva para el pronóstico de
eventos y fenómenos, a lo largo de las décadas se ha evidenciado un incremento
significativo de investigaciones en el campo de la educación que involucren
redes neuronales artificiales como herramienta para dar solución a problemas
que acechan la formación académica de los estudiantes. Es así como en la década
del 70 se inician las primeras investigaciones que dan origen a programadas de
tutorías y aprendizajes automatizados mediante redes neuronales y sistemas
expertos orientados al seguimiento y evaluación de estudiantes y docentes, los
resultados no fueron los esperados por los investigadores, pero significó el
punto de partida para investigaciones posteriormente exitosas (John Seely Brown
y Burton, 1978; J.S. Brown y Burton, 1978; Gable y Page, 1980; Goldstein y
Papert, 1977; Self, 1979). La década de los 80 y 90 se caracterizó por el
perfeccionamiento y adaptación de las diversas herramientas de la IA en
investigaciones dentro del campo de la educación, la aplicación de los sistemas
de tutoría automatizados y los resultados en la predicción mejoraron
considerablemente como consecuencia de perfeccionamiento e implementación de
nuevos algoritmos computacionales (Boden, 1984; Salchenberger, 1989;
Schaufelberger, 1993; Siemer y Angelides, 1998; Wasson, 1997).
En este nuevo milenio las investigaciones en
educación utilizando RNA a tomado notoriedad, entre ellas podemos mencionar la
realizada por Çetinkaya y Baykan (2020) en Rusia, en la que implementaron un
modelo de RNA para pronosticar el talento de los estudiantes en programación
utilizando tres algoritmos computacionales implementados en el MATLAB, así
mismo Álvarez et al. (2016) en Cuba mediante una RNA pronosticaron el
rendimiento académico de los estudiantes correspondientes al curso de
Estructura de Datos I y II, en la república de Chile Zambrano et al. (2011) mediante RNA y Data Warehouse
pronosticó el rendimiento académico de los estudiantes de Ingeniería Civil de
la Universidad de Atacama utilizando datos históricos.
Esta investigación se justifica en la
necesidad de diseñar e implementar un modelo de red neuronal artificial que
permita predecir los resultados académicos de los estudiantes antes de culminar
el semestre académico, con la finalidad de que el docente utilicé técnicas y
estrategias de aprendizaje adecuadas para mejorar los posibles resultados
académicos obtenidos por sus estudiantes.
METODOLOGÍA
Los
datos que alimentaron la capa de entrada de la RNA se obtuvieron mediante la
técnica de la encuesta aplicada a 50 estudiantes de la carrera profesional de
Ingeniería Civil que ya aprobaron la asignatura de Física, se utilizó como
instrumento un cuestionario con un coeficiente de confiabilidad de Alpha de
Cronbach de 0.854, las preguntas que conforman el cuestionario son 18 y responden a los factores de orden cognitivo
(9), emocional (6) y socio cultural (3)
que influyen en el rendimiento académico de los estudiantes. Las 18 preguntas
recolectan información referida a planes de estudios, nivel educativo de los
padres, servicios de internet, características demográficas, calificaciones
obtenidas en el primer ciclo en asignaturas que son pre requisitos para Física,
calificaciones obtenidas en la secundaria, calificación obtenida en el examen
de admisión, el autoconcepto académico, la vocación, la motivación, sexo, edad,
estado civil, carga familiar, consumo de drogas, consumo de alcohol.
Se utilizó el diseño metodológico CRIS-DM,
primero se identificó el problema y las variables de estudio, se elaboró el
instrumento de recolección de datos y se procedió a la recolección, selección y
preparación de los mismos, luego se diseñó la arquitectura de la red neuronal
artificial, se validó el modelo de RNA implementado tomando un porcentaje de
los datos para el entrenamiento, la validación y la prueba utilizando los
algoritmos Scaled Conjugate Gradient y
Levenberg-Marquardt , los algoritmos se ejecutaron 10 veces por cada número de
neuronas en la capa oculta, el número de neuronas en la capa oculta variaba
entre 2 y 50 neuronas, se trataba de
buscar que el error cuadrático medio (MSE) sea lo más cercano a cero y el
coeficiente de correlación (R) sea lo más cercano a uno, siendo:
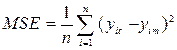

Donde “n” es el número de observaciones, yic
es el i-ésimo valor calculado, yim es el i-ésimo valor medido,
finalmente ym es el valor medio de los valores calculados.
Figura
1
Diagrama
secuencial del diseño metodológico

RESULTADOS
Y DISCUSIÓN
Los
mejores resultados en la implementación de la red neuronal se obtuvieron al
emplear el 85% de los datos para el entrenamiento (training), el 10% para la
validación (validation) y el 5% para la prueba (test), se efectúo 10 corridas
para cada algoritmo de aprendizaje, con 14 neuronas en la capa oculta para el
Levenberg-Marquardt y 50 neuronas en la capa oculta para el Scaled Conjugate
Gradient. La Tabla 1 detalla los valores obtenidos en el MSE y en el R de las
redes neuronales con respecto a cada algoritmo de aprendizaje y al número de
neuronas en la capa oculta (N° nco), la
Figura 2 y la Figura 3 muestran los diagramas de las redes neuronales
implementadas para cada algoritmo, la Figura 4 y la Figura 5 muestran el
R-Training, R-Validation y el R-Test de ambos algoritmos, la Figura 6 y la
Figura 7 muestran el histograma de error para los dos algoritmos, la Figura 8 y
la Figura 9 muestran el rendimiento de
ambos algoritmos.
Tabla 1
Análisis de los resultados
|
Algoritmo |
NN° nco |
Entrena-miento
(Training-R) |
Validación (Validation-R) |
Prueba (Test-R) |
All-R |
Entrenamiento (Training -MSE) |
Validation (Validation-MSE) |
Prueba (Test-MSE) |
|
Levenberg-Marquardt |
114 |
0.99994 |
0.87178 |
0.95254 |
0.96723 |
0.00000389003 |
0.00264181 |
0.0138162 |
|
Scaled
Conjugate Gradient |
550 |
0.98114 |
0.94263 |
0.759620 |
0.76359 |
0.00043774 |
0.0951 |
0.0990 |
Fuente: elaboración propia
|
Figura
2 Diagrama
de la red neuronal- Levenberg-Marquardt |
|
Figura 3 Diagrama
de la red neuronal- Scaled Conjugate Gradient |
|
|
|
|
|
Nota. Red neuronal artificial implementada
indicando el número de neuronas en cada capa. |
|
Nota. Red neuronal artificial implementada
indicando el número de neuronas en cada capa. |
|
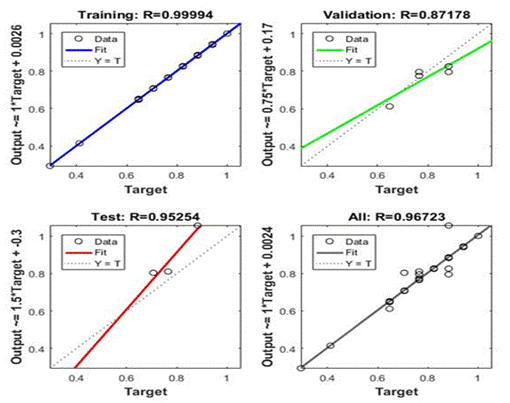
Figura 4 R del Levenberg-Marquardt |
|
Figura
5 R del Scaled Conjugate Gradient. |
|
|
|
|
|
|
|
|
|
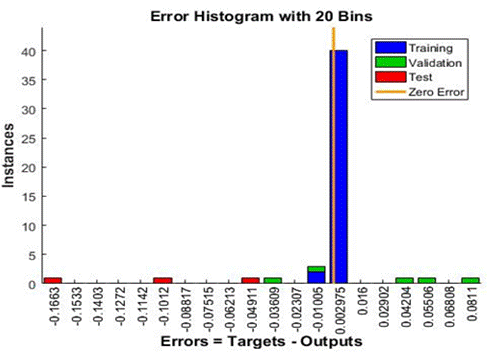
Figura 6 Histograma de error del Levenberg-Marquardt |
|
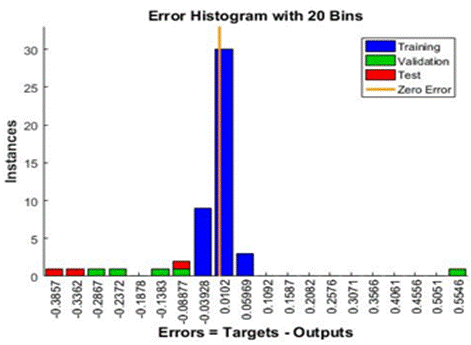
Figura
7 Histograma de error del Scaled Conjugate
Gradient |
|
|
|
|
|
Figura
8 Rendimiento
del Levenberg-Marquardt |
|
Figura 9 Rendimiento
del Scaled Conjugate Gradient. |
|
|
|
|
Tabla 2
Pronóstico de promedios finales
|
Promedios finales reales |
Pronóstico |
|
|
LM |
SCG |
|
|
11 |
11 |
17 |
|
13 |
13 |
12 |
|
15 |
15 |
15 |
|
14 |
14 |
14 |
|
11 |
11 |
11 |
|
15 |
15 |
14 |
|
13 |
13 |
13 |
|
14 |
14 |
13 |
|
13 |
13 |
13 |
|
17 |
17 |
17 |
|
12 |
12 |
12 |
|
15 |
14 |
15 |
|
13 |
13 |
13 |
|
15 |
14 |
15 |
|
13 |
13 |
13 |
|
16 |
16 |
15 |
|
16 |
16 |
16 |
|
15 |
15 |
15 |
|
13 |
14 |
13 |
|
12 |
12 |
11 |
|
14 |
14 |
14 |
|
12 |
14 |
12 |
|
15 |
15 |
15 |
|
13 |
13 |
13 |
|
11 |
11 |
11 |
|
14 |
14 |
14 |
|
14 |
14 |
14 |
|
11 |
11 |
11 |
|
14 |
14 |
16 |
|
11 |
11 |
16 |
|
11 |
11 |
15 |
|
12 |
12 |
19 |
|
12 |
12 |
12 |
|
15 |
15 |
15 |
|
13 |
13 |
13 |
|
14 |
14 |
14 |
|
11 |
11 |
12 |
|
11 |
11 |
13 |
|
14 |
14 |
14 |
|
13 |
14 |
13 |
|
5 |
5 |
-5 |
|
11 |
11 |
11 |
|
11 |
10 |
11 |
|
7 |
7 |
8 |
|
12 |
12 |
12 |
|
15 |
18 |
16 |
|
13 |
13 |
13 |
|
12 |
12 |
12 |
|
12 |
12 |
12 |
|
11 |
11 |
11 |
|
% del pronóstico |
86% |
70% |
Fuente:
elaboración propia
En la Tabla 1 se puede observar que, de los
dos algoritmos, el Levenberg-Marquardt con 14 neuronas da mejores resultados en
la predicción en menor tiempo tal como lo afirma Hagan y Menhaj (1994). Se
puede observar: Training-R = 0.99994, Validation-R = 0.87178, Test-R = 0.95254,
All-R = 0.96723, Training-MSE =0.00000389003, Validation-MSE = 0.00264181,
Test-MSE = 0.0138162.
En el histograma de error se simboliza el
entrenamiento de los datos, las barras verdes representan la validación de los
mismos y las barras rojas la prueba de los datos, en el caso del algoritmo
Levenberg-Marquardt la mayoría de los errores se encuentra entre -0.1012 y
0.05506, se pueden observar un valor atípico en -0.1663 y en 0.0811, en el caso
del algoritmo Scaled Conjugate Gradient la mayoría de los errores se encuentran
ubicados entre -0.3857 y 0.05969 , se puede observar un valor atípico en
0.5546. La Tabla 2 muestra que la red entrenada por medio del algoritmo
Levenberg-Marquardt (LM) tiene una capacidad de predicción del 86%, y la red
entrenada por medio del algoritmo Scaled Conjugate Gradient (SCG) tiene una
capacidad de predicción del 70%.
CONCLUSIONES
El
modelo de red neuronal artificial implementada en esta investigación no debe
ser tomada como válida en otra universidad puesto que las características de
orden cognitivo, emocional y socio cultural es propio de cada población y varía
de acuerdo a las condiciones de espacio-tiempo. No obstante, la metodología,
antecedentes de estudio y los criterios para el diseño de la arquitectura de la
RNA pueden considerarse para investigaciones dentro del contexto local,
regional, nacional e internacional.
Se ha demostrado que las RNA constituyen una
herramienta poderosa de predicción, la red entrenada por medio del algoritmo
Levenberg-Marquardt (LM) tiene una capacidad de predicción del 86%, y la red
entrenada por medio del algoritmo Scaled Conjugate Gradient (SCG) tiene una
capacidad de predicción del 70%, lo cual resulta beneficioso para la comunidad
estudiantil, pues le permite al docente conocer los posibles resultados
académicos de sus estudiantes antes de culminar el semestre académico y de esta
manera aplicar técnicas y estrategias a fin de mejorar el logro de competencias
de sus estudiantes.
Se evidencia también que para lograr un alto
porcentaje en la predicción es importante tener en cuenta que el coeficiente de
confiabilidad del Alpha de Cronbach sea los más cercano a uno, que la red
neuronal artificial implementada debe ser entrenada tantas veces sea necesario
teniendo en cuenta el número de neuronas en la capa oculta y el algoritmo de
entrenamiento. Una limitación en esta investigación es la cantidad de datos, no
obstante, a quedado demostrado que la RNA implementada es capaz de proporcionar
un alto índice de porcentaje de predicción.
REFERENCIAS
BIBLIOGRÁFICAS
Álvarez, J., Lau, R., Pérez, S., y Leyva, E. C.
(2016). Predicción de resultados académicos de estudiantes de informática
mediante el uso de redes neuronales. Ingeniare.
Revista chilena de ingeniería, 24(4),
715-727. https://doi.org/10.4067/S0718-33052016000400015
Amershi, S., Arksey, N., Carenini, G., Conati, C.,
Mackworth, A., Maclaren, H., y Poole, D. (2005). Designing CIspace: Pedagogy
and usability in a learning environment for AI. Proceedings of the 10th Annual SIGCSE Conference on Innovation and
Technology in Computer Science Education
- ITiCSE ’05, 178. https://doi.org/10.1145/1067445.1067495
Aranda-Corral, G. A., Calmet, J., y Martín-Mateos, F.
J. (Eds.). (2014). Artificial
Intelligence and Symbolic Computation (Vol. 8884). Springer International
Publishing. https://doi.org/10.1007/978-3-319-13770-4
Boden, M. A. (1984). Impacts of artificial
intelligence. Futures, 16(1), 60-70.
https://doi.org/10.1016/0016-3287(84)90007-7
Brazdil, P., y Jorge, A. (Eds.). (2001). Progress in Artificial Intelligence:
Knowledge Extraction, Multi-agent Systems,Logic Programming, and Constraint
Solving (Vol. 2258). Springer Berlin Heidelberg. https://doi.org/10.1007/3-540-45329-6
Brown, John Seely, y Burton, R. R. (1978). A
paradigmatic example of an artificially intelligent instructional system. International Journal of Man-Machine Studies,
10(3), 323-339. https://doi.org/10.1016/S0020-7373(78)80050-9
Brown, J.S., y Burton, R. R. (1978). Diagnostic models
for procedural bugs in basic mathematical skills. Cognitive Science, 2(2),
155-192. Scopus. https://doi.org/10.1016/S0364-0213(78)80004-4
Brusilovsky, P., y Peylo, C. (2003). Adaptive and
intelligent web-based educational systems. International
Journal of Artificial Intelligence in Education, 13(2-4), 159-172. Scopus. https://www.scopus.com/inward/record.uri?eid=2-s2.0-85013582692&partnerID=40&md5=8fd4cfe2d1364a872d3b599134c1f432
Cerda, G., Pérez, C., Elipe, P., Casas, J. A., y Del
Rey, R. (2019). Convivencia escolar y su relación con el rendimiento académico
en alumnado de Educación Primaria. Revista
de Psicodidáctica, 24(1), 46-52. https://doi.org/10.1016/j.psicod.2018.05.001
Çetinkaya, A., y Baykan, Ö. K. (2020). Prediction of
middle school students’ programming talent using artificial neural networks. Engineering Science and Technology, an
International Journal. https://doi.org/10.1016/j.jestch.2020.07.005
Edel, R. (2003). Factores asociados al rendimiento
académico. Revista Iberoamericana de Educación,
33(1), 1-20. https://doi.org/10.35362/rie3312872
Gable, A., y Page, C. V. (1980). The use of Artificial
Intelligence techniques in Computer-Assisted Instruction: An overview. International Journal of Man-Machine Studies,
12(3), 259-282. https://doi.org/10.1016/S0020-7373(80)80028-9
Garbanzo, G. M. (2007). Factores asociados al
rendimiento académico en estudiantes universitarios, una reflexión desde la
calidad de la educación superior pública. Revista
Educación, 31(1), 43-63. https://www.redalyc.org/articulo.oa?id=44031103
Garrido, A. (2010). Mathematics and Artificial
Intelligence, two branches of the same tree. Innovation and Creativity in Education, 2(2), 1133-1136. https://doi.org/10.1016/j.sbspro.2010.03.160
Goldstein, I., y Papert, S. (1977). Artificial
intelligence, language, and the study of knowledge. Cognitive Science, 1(1),
84-123. https://doi.org/10.1016/S0364-0213(77)80006-2
Pinto, P. M., Fernández, Y. O., y Cabezas, N. G.
(2020). Intercultural education in the process of educational humanization of
college students: Influences on academic achievement. Interciencia, 45(4),
201-208. Scopus. https://www.scopus.com/inward/record.uri?eid=2-s2.0-85085116052&partnerID=40&md5=d5452e892f20e1b42dfe7f487dd4ba51
Popenici, S. A. D., y Kerr, S. (2017). Exploring the
impact of artificial intelligence on teaching and learning in higher education.
Research and Practice in Technology
Enhanced Learning, 12(1). Scopus.
https://doi.org/10.1186/s41039-017-0062-8
Salanova, M., Cifre, E., Grau, R. M., Llorens, S., y
Martínez, I. M. (2005). Antecedentes de la autoeficacia en profesores y
estudiantes universitarios: Un modelo causal. Revista de Psicología del Trabajo y de las Organizaciones, 21, 18.
Salchenberger, L. (1989). A strategy for integrating
artificial intelligence technology into a graduate business curriculum. Education and Computing, 5(3), 189-196. https://doi.org/10.1016/S0167-9287(89)80042-1
Samani, T., Porayska-Pomsta, K., y Luckin, R. (2017). Bridging the gap between high and low
performing pupils through performance learning online analysis and curricula:
Vol. 10331 LNAI (p. 655). Scopus. https://doi.org/10.1007/978-3-319-61425-0_82
Schaufelberger, W. (1993). Low cost control education
software for MS-DOS PCs. Automatica, 29(6), 1501-1516. https://doi.org/10.1016/0005-1098(93)90013-J
Self, J. A. (1979). Student models and artificial
intelligence. Computers & Education,
3(4), 309-312. https://doi.org/10.1016/0360-1315(79)90008-3
Siemer, J., y Angelides, M. C. (1998). A comprehensive
method for the evaluation of complete intelligent tutoring systems. Decision Support Systems, 22(1), 85-102. https://doi.org/10.1016/S0167-9236(97)00033-X
Vila, E. M. S., y Penín, M. L. (2007). Introduction to
special issue AI techniches applied in education. Inteligencia Artificial, 11(33),
7-12. Scopus. https://www.scopus.com/inward/record.uri?eid=2-s2.0-36049016227&partnerID=40&md5=7a181a22f3b187c2e99100dbedea61e5
Wasson, B. (1997). Advanced educational technologies:
The learning environment. Norwegian
Perspectives on Computing in Complex Domains, 13(4), 571-594. https://doi.org/10.1016/S0747-5632(97)00027-7
Zambrano, C., Rojas, D., Carvajal, K., y Acuña, G. (2011).
Análisis de rendimiento académico estudiantil usando data warehouse y redes
neuronales. Ingeniare. Revista chilena de
ingeniería, 19(3), 369-381. https://doi.org/10.4067/S0718-33052011000300007