Veritas Et Scientia
Vol.
10. N° 1
Enero
- junio del 2021
ISSN
Edición Online: 2617-0639
DOI:
https://doi.org/10.47796/ves.v10i1.461
ARTÍCULO
ORIGINAL
MODELO “ARIMA” SOBRE EL CONSUMO DE AGUA DE USO
POBLACIONAL EN LA CIUDAD DE TACNA
“ARIMA” MODEL ON THE CONSUMPTION OF WATER FOR
POPULATION USE IN THE CITY OF TACNA
Limache
Sandoval, Elmer Marcial [1]
![]() https://orcid.org/0000-0003-4852-1916
https://orcid.org/0000-0003-4852-1916
Aceptado:
07/05/2021
Publicado online:30/05/2021
![]()
RESUMEN
El objetivo fue construir un
modelo de pronóstico de series de tiempo en base a patrones y variables
endógenas del consumo del agua potable y adicionalmente determinar la
tendencia, estacionalidad, los patrones cíclicos y las características del agua
que se consume en la ciudad de Tacna para la obtención de pronósticos. La
investigación fue no experimental, correlacional y longitudinal, con
información de periodicidad mensual entre enero de 2006 hasta marzo de 2018
registrada mediante análisis documental. La unidad de análisis fueron las
unidades económicas de la ciudad de Tacna con servicio de agua potable
conectado a la red pública y consumo mensual como variable de interés. La
población corresponde a una serie finita de datos mensuales de tamaño N=383 meses.
La muestra estuvo constituida por 139 observaciones entre enero 2006-julio 2017
con los que se ha construido el modelo ARIMA en base a la metodología
Box-Jenkins y extendida hasta marzo de 2018, para la validación del modelo. La
conclusión principal es la obtención del modelo de pronóstico para el consumo
de agua de uso poblacional en la ciudad de Tacna ARIMA (0,1,1)(0,1,1)12 con
intercepto y cuya formulación matemática empírica es:
![]()
con patrones de tendencia y estacionalidad.
Palabras clave: Modelos ARIMA, series de tiempo,
patrones de datos, pronósticos.
ABSTRACT
The objective was to
build a time series forecast model based on endogenous patterns and variables
of drinking water consumption and additionally determine the trend,
seasonality, cyclical patterns and characteristics of the water consumed in the
city of Tacna for the obtaining forecasts. The research was non-experimental,
correlational and longitudinal, with monthly information from January 2006 to
March 2018 recorded through documentary analysis. The unit of analysis were the
economic units of the city of Tacna with drinking water service connected to
the public network and monthly consumption as variable of interest. The
population corresponds to a finite series of monthly data of size N = 383
months. The sample consisted of 139 observations between January 2006-July 2017
with which the ARIMA model has been built based on the Box-Jenkins methodology
and extended until March 2018, for the validation of the model. The main
conclusion is the obtaining of the forecast model for the consumption of water
for population use in the city of Tacna ARIMA (0,1,1) (0,1,1) 12 with intercept
and whose empirical mathematical formulation is:
![]()
with trend and
seasonality patterns.
Keywords: ARIMA models, time series, data patterns,
forecasts..
![]()
INTRODUCCIÓN
El agua es un recurso escaso por el
que millones de personas luchan diariamente para proveerse de él (ONU-AGUA,
2005, p.3) y Rodriguez-Villamil (2013) sostiene que las familias atraviesan
dificultades y rutinas para obtener, transportar, almacenar, cuidar y usar el
agua y que, en muchos casos es de mala calidad afectando su salud y seguridad
alimentaria. El crecimiento poblacional incentiva el crecimiento de las
ciudades y el incremento del consumo del agua dulce, recurso no renovable. “Las
poblaciones crecen y se desarrollan generalmente dentro y alrededor de fuentes
naturales básicas e imprescindible para su crecimiento y desarrollo siendo una
de ellas el Agua” (Rosasco, 2006)
En la última década, en América Latina
y el Caribe se ha asistido a una significativa reducción de la pobreza. Sin
embargo, más de 160 millones de personas continúa en la pobreza y el promedio
de los niveles de abastecimiento de agua y saneamiento en la región son a los
de otros países en desarrollo y, los niveles reales de acceso a los servicios
son inferiores y se aprecian graves deficiencias en la calidad del servicio que
afectan a las áreas rurales y a los pobres (ONU-AGUA, 2015. p 10). El estudio del consumo de agua es importante y
constituye un elemento importante en la dieta pues los individuos no pueden
estar sometidos a privaciones por largos períodos sin tener efectos importantes
en su salud, aun cuando se muestra recuperación del peso corporal cuando la
restricción termina (Lopez-Espinoza, Ríos y Soto, 2004). Pero, las empresas que
administran el agua de uso poblacional, reconocen que contiene elementos
contaminantes (Mendez y Feliciano, 2010; EPS TACNA, 2018) y que muchas de ellas
no reutilizan las aguas residuales, lo cual ahorraría costos en los programas
de producción de agua, que podría ser utilizada en parques y jardines (Mendez y
Feliciano, 2010).
En Tacna, zona de escasez hídrica, el
uso racional del agua es de vital importancia, con 341,838 habitantes y una
tasa de crecimiento de 4.068 (INEI, 2009) y la ubica entre las ciudades de
mayor crecimiento en el país. Asimismo, para el año 2014 el consumo de agua de
uso doméstico fue de 9 949 000 metros cúbicos para una población de 312311
(INEI, 2010, p. 106) con un consumo promedio 31.85 metros cúbicos inferior al
recomendado por la Organización Mundial de la Salud y por debajo del consumo
promedio nacional.
El consumo irracional origina desperdicios
del agua tratada con el consiguiente costo para la sociedad estimándose que la
EPS Tacna pierde el 21,9% del agua que procesa (EPS Tacna, 2009), situación a
solucionarse en el corto plazo. Asimismo, el agua es de mala calidad, aun
después del tratamiento correspondiente. El agua de la cuenca Caplina que
abastece de agua a la ciudad contiene índices de boro, arsénico hierro y
aluminio por encima de los permitidos para el consumo humano (Región Tacna,
2016, p.60-64). El agua es un bien de demanda inelástica, por tanto, de consumo
imprescindible para las familias.
Hay varios enfoques sobre el consumo
del agua, siendo uno de ellos el del comportamiento del consumidor que toma en
cuenta factores diferentes según los autores, y sostiene que hay factores
externos, del medio ambiente y factores internos, que dependen del individuo
que los que determinan el consumo de un bien. Otro enfoque proviene de la
teoría económica y que sostiene que el consumo de un bien depende del precio
del bien, del ingreso y del precio de los bienes relacionados. El conocimiento
de estos factores y la influencia que tienen en el consumo, así como las
variables que intervienen en el consumo es importante en el caso de Tacna en el
cual el bien que se utiliza es escaso y con características particulares siendo
un tema siempre vigente y que merece ser estudiado.
Se han desarrollado modelos de demanda
de agua que incluyen variables de tipo cuantitativo y cualitativo con la
finalidad de realizar pronósticos y proyecciones, o para describir el mecanismo
del consumo de este bien, realizado en otras realidades, por lo que es
necesario determinar los factores que determinan el consumo del agua y realizar
los pronósticos adecuados en base a este conocimiento, proporcionando así a los
organismos operadores de la distribución de agua instrumentos que permitan
gestionar adecuadamente este recurso.
Por otro lado, en el intento de
modelizar la demanda de agua se han diseñado propuestas como el de Clavijo
(2013) que utiliza variables de consumo, ingreso y número de habitantes, Olmeda
(2013) que utiliza un modelo econométrico con variable endógena el crecimiento
medio del PBI, variables exógenas como inversión, capital humano y tasa de
utilización del agua mediante mínimos cuadrados ordinarios. Henao y Córdova
(2007) hace hincapié en los factores externos en la explicación del consumo de
agua como los factores sociales, demográficos y económicos.
Por ello, la investigación busca
construir un modelo de pronóstico de series de tiempo en base a patrones y
variables endógenas del consumo del agua potable en la ciudad de Tacna,
determinar la tendencia en el pronóstico de series de tiempo en el consumo del
agua potable en la ciudad de Tacna, determinar la estacionalidad en el
pronóstico, determinar los patrones cíclicos en el pronóstico de series de
tiempo, así como determinar las características del agua potable que consume la
población en la ciudad de Tacna.
En base al comportamiento de los
consumos de bienes y al crecimiento poblacional se plantea la hipótesis que el
modelo de pronóstico de series de tiempo con variables de consumo rezagadas en
el tiempo considerando patrones de tendencia creciente y estacionalidad mensual
aplicado al consumo de agua de uso poblacional en la ciudad de Tacna basado en
la metodología Box Jenkins es el adecuado en el caso de Tacna.
METODOLOGÍA
La Investigación es no experimental,
correlacional y longitudinal, con información registrada en intervalos
sucesivos en el tiempo originando una serie de periodicidad mensual entre enero
de 2006 hasta marzo de 2018 registrada mediante análisis documental (Hernandez
Sampieri, 2014. pp.154-162). El esquema que relaciona la variable dependiente
(consumo de agua potable en la ciudad Tacna) e independiente (variables
rezagadas de esta misma variable) es:
|
Variables rezagadast-k |
|
Consumo de agua potablet |
La unidad de análisis la conforman las
unidades económicas de la ciudad de Tacna que tienen el servicio de agua
potable conectados a la red pública de abastecimiento. El consumo mensual de agua
de estas unidades económicas, medidas en metros cúbicos (m3), es la variable de
interés para el estudio y para el cual se busca la construcción de un modelo de
pronóstico.
La población corresponde a una serie
finita de datos mensuales ordenados en el tiempo de tamaño N=383 meses
relacionado al consumo de agua potable en la ciudad de Tacna desde el mes de
diciembre de 1985 hasta el mes de marzo de 2018 que es el período de referencia
con información de la EPS Tacna desde su creación como SEDATACNA. La muestra
está constituida por la serie de tiempo de datos mensuales de 139 observaciones
entre enero 2006-julio 2017 con los que se ha construido el modelo ARIMA, a los
que se adiciona las observaciones de agosto 2017 hasta marzo de 2018 para la
idoneidad del modelo, haciendo un total de 147 observaciones muestrales hasta
ese momento, ordenadas en el tiempo.
El método de muestreo fue no
aleatorio, y la técnica por conveniencia, por la disposición de la información
registrada a partir de enero de 2006 hasta marzo de 2018.
Los datos de la serie de tiempo de la
variable Consumo Mensual de Agua Potable se recolectaron mediante análisis
documental y se incorporaron a una matriz de datos utilizando el paquete
estadístico SPSS 25. La información fue verificada respecto a calidad de los
datos lográndose ello al momento de graficar un diagrama secuencial de todos
los datos originales. Las técnicas estadísticas que se utilizaron fueron el
análisis de correlación y el modelamiento de series temporales mediante la
metodología Box-Jenkins. Dado que el nivel de investigación es explicativa, en
primer lugar, se realizó el análisis de autocorrelación, utilizando el
estadístico de autocorrelación rk, condición previa para la aplicación de la
técnica principal de análisis que son los modelos ARIMA, en conjunción con los
dispositivos gráficos como los correlogramas, diagramas de secuencia y
diagramas de dispersión, que permitieron apreciar los patrones de las series de
tiempo como tendencia, estacionalidad, patrones cíclicos e irregularidad.
En todos los casos el Error tipo I, la
probabilidad de rechazar la hipótesis nula fue el 5%.
Para las relaciones de dependencia, es
decir, el análisis de regresión entre el Consumo mensual y las variables
rezagadas se utilizaron los modelos autorregresivos integrados de media móvil
con estacionalidad s, ARIMA (p,d,q)(P,D,Q)s de media móvil y autorregresivos de
órdenes p, d, q correspondientes a la parte regular de la serie de tiempo y P,
D, Q correspondientes a la parte estacional de la serie, siguiendo la
metodología propuesta por Ferrán (1997).
Las tablas estadísticas fueron
utilizadas para la presentación de las autocorrelaciones, la significancia y
los principales estadísticos y los diagramas secuenciales que presentaron las
series de tiempo según su secuencia de ocurrencia en el tiempo para la
visualización que permita detectar los patrones de la serie. Otra herramienta
gráfica fueron los correlogramas que permiten visualizar las autocorrelaciones
para varios desfases de la serie.
RESULTADOS
El diagrama secuencial de la Figura 1
muestra una tendencia creciente del Volumen Facturado Total de Agua Potable en
la ciudad de Tacna con dos valores extremos máximos entre mayo del 2012 y mayo
del 2013 y los valores extremos mínimos se encuentran entre junio del 2009 y
noviembre del 2011.
Figura 1
Tacna: Diagrama
de Volumen Facturado Total
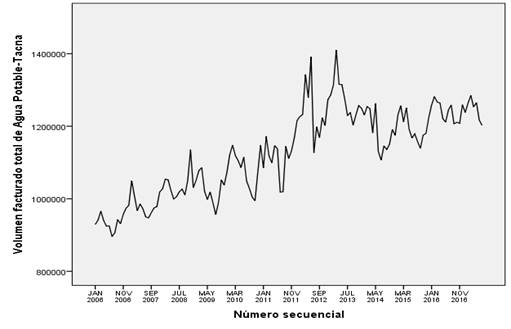
Fuente:
EPS Tacna (2017)
Modelo ARIMA de volumen facturado de
agua potable
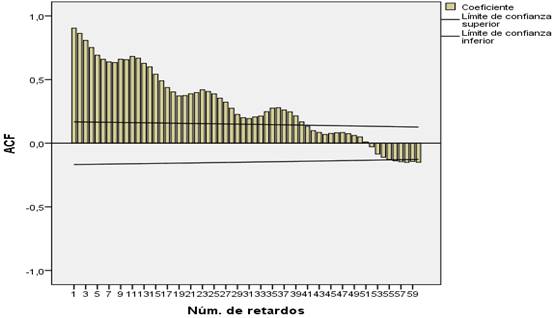
El análisis de las autocorrelaciones
las muestra en orden descendente y todas significativas, siendo positivas hasta
el período 51, para posteriormente, a partir del período 52 ser negativas,
siempre significativas, como se muestra en el correlograma.
El comportamiento descendente de las
autocorrelaciones simples indica un patrón de tendencia y el comportamiento
ondulante descendente un patrón de estacionalidad mensual.
Figura 2
Tacna: Sesenta
primeras autocorrelaciones de Volumen Facturado Total de Agua Potable.
El reporte de la prueba de
homogeneidad de varianzas del Volumen Facturado Total de Agua Potable mediante
el estadístico de Levene rechaza la Hipótesis Nula con p=0,016 que evidencia
que la serie no tiene varianza constante y los datos requieren transformarse.
Para la transformación se usó la de Box-Cox (Ferrán, 1997) y dado el poder de
transformación de -1,059 comparado con el múltiplo de ½ más cercano indica que
es p=0, y la transformación aplicable el logaritmo natural de la serie, sobre
el cual se realizaron los análisis subsiguientes.
Las primeras sesenta autocorrelaciones
de la serie transformada Ln Xt determina que son significativas y con signo
positivo hasta el retardo 51 para luego ser negativas a partir del retardo 52.
Sin embargo, el comportamiento de la serie de autocorrelaciones simples,
alrededor de los retardos periódicos, permite inferir que hay un patrón de
tendencia en los datos originales, aun cuando se aprecia también que la
disminución de los valores de las autocorrelaciones no es brusca, pues cada
cierto número de retardos, como el 11, el 23, el 36 y el 47 alcanzan valores
altos.
El correlograma de las sesenta
autocorrelaciones simples permite apreciar el comportamiento descendente de
ellas y muestra tendencia en la serie transformada. Asimismo, el comportamiento
ondulante con picos altos y bajos a lo largo de su trayectoria con repuntes en
los retardos 11, 23, 36 y 47 indica una estacionalidad mensual en forma similar
al comportamiento de los datos no transformados.
El análisis de las autocorrelaciones
simples con diferenciación de grado 1 (d=1) de la serie transformada Ln Xt del
Volumen Facturado Total de Agua Potable las cuales son significativas al 1%,
excepto la del retardo 4 que es significativa al 5%. El análisis de las
autocorrelaciones de la parte regular de la serie permite apreciar que la
autocorrelación del retardo 1 (r=-0.290) al realizarse la prueba de hipótesis
de significancia, es significativa (Zc= -3.42).
Como el valor crítico Z=1.96 a una
confianza del 95%, entonces la decisión estadística indica que la
autocorrelación en el retardo 1 es significativa. No ocurre lo mismo con la
autocorrelación en el retardo 2, r2=0,034 cuya Zc=0.40, con lo cual no se
rechaza la H0 pudiéndose afirmar que no es significativa, y, en general, ocurre
con las subsiguientes autocorrelaciones de la parte regular r3, r4, r5, r6, r7,
r8, r9 y r10, que es donde se analiza la tendencia.
Por lo tanto, la diferenciación de
orden 1 (d=1) ha eliminado la tendencia de la serie convirtiendo los datos en
estacionarios en la media.
Figura 3
Correlograma de
60 primeras Autocorrelaciones de retardos periódicos
del Volumen
Facturado Total de Agua Potable con D=1
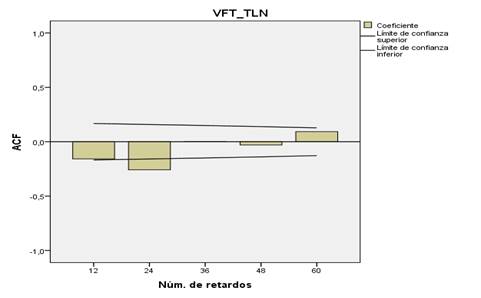
Para el tratamiento de la
estacionalidad se analizaron las autocorrelaciones de la parte estacional de la
serie que muestra las sesenta primeras autocorrelaciones a las cuales se aplicó
diferenciación estacional de grado 1 (D=1) con la finalidad de estabilizar la
serie o eliminar la estacionalidad. El correlograma de las autocorrelaciones
periódicas mostradas en la figura 3 confirma que la autocorrelación del período
24 es significativa lo cual es un indicio que la diferenciación estacional 1
(D=1) no ha sido suficiente para eliminar la estacionalidad.
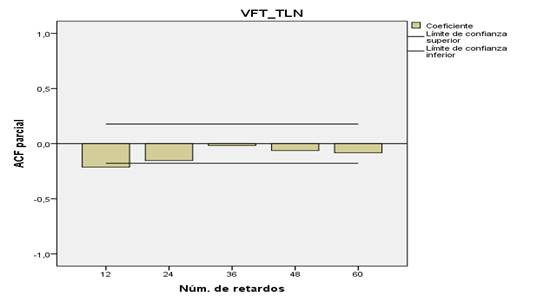
En el proceso para la determinación
del parámetro D se calcularon las autocorrelaciones en los retardos periódicos
utilizando diferenciación estacional de grado 2 (D=2) que se muestran en la
tabla 1 y que permite determinar que las autocorrelación r12 = -0,443 es significativa
y las subsiguientes r24, r36, r48 y r60 no lo son, indicio que esta
diferenciación estacional eliminó la estacionalidad en la serie transformada,
de lo que puede colegirse que D=2 es el parámetro seleccionado.
Tabla 1
Autocorrelaciones
en los retardos periódicos del Volumen Facturado Total de Agua Potable con D=2
|
Retardo |
Autocorrelación |
Típ. Errora |
Estadístico de Box-Ljung |
||
|
Valor |
gl |
Sig.b |
|||
|
12 |
-,443 |
,087 |
118,071 |
12 |
,000 |
|
24 |
-,146 |
,082 |
150,462 |
24 |
,000 |
|
36 |
,075 |
,077 |
203,147 |
36 |
,000 |
|
48 |
-,034 |
,071 |
225,858 |
48 |
,000 |
|
60 |
,104 |
,064 |
238,348 |
60 |
,000 |
A continuación, el proceso de
estabilización se realizó en forma simultánea en la tendencia y en la
estacionalidad al utilizarse diferenciación regular (d=1) y diferenciación
estacional (D=1) como se muestra en la tabla 14. Al analizar las autocorrelaciones
de la parte regular se visualiza que las autocorrelaciones r1, y r11 son las
autocorrelaciones significativas. Al analizar las autorrelaciones en los
retardos periódicos se observa que r1 es significativa, así como r11, r12, de
lo que se infiere que probablemente el grado de la diferenciación regular se
podría establecer en d=1 y la diferenciación estacional en D=1.
Resumiendo, los grados de
diferenciación a considerar en la determinación del modelo serán: Para la
diferenciación regular: d=1 y d=2. Para la diferenciación estacional: D=1 y
D=2.
Figura 4
Correlograma de
60 autocorrelaciones del Volumen Facturado Total de Agua Potable
con d=1
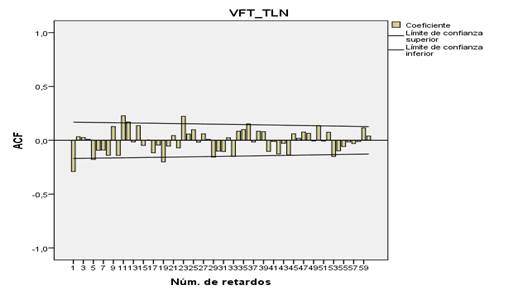
Determinación de los órdenes de p y q
Los órdenes p y q del modelo ARIMA se
determinan del análisis de las autocorrelaciones simples y parciales de la
parte regular, es decir, en las autocorrelaciones r1 a r11. Así, el análisis de
las autocorrelaciones de la parte regular indica que la autocorrelación 1,
r1=-0,290, es significativa, conjuntamente con la autocorrelación 11,
r11=0,229), sugiriendo que podría tratarse de un modelo de media móvil (MA) de
órdenes 1 o 2 (q=1 o q=2). No se aprecia el comportamiento decreciente de las
iniciales autocorrelaciones hasta llegar a ser nulas, típico de los modelos
autorregresivos (AR) (Fig. 4)
El análisis de las sesenta
autocorrelaciones parciales, permite visualizar que las autocorrelaciones de
los retardos 1, 5, 6, 7, 8 y 10 son significativas y el resto no, definiendo un
crecimiento y decrecimiento en el recorrido.
Este comportamiento permite inferir
que se trata de un modelo autorregresivo de media móvil (ARMA), cuyos órdenes
son variados: p=1, p=2 y p=3 en la parte autorregresiva (Fig. 5).
De lo anteriormente analizado resulta
que los posibles órdenes de p en la parte regular de la serie correspondiente
al modelo autorregresivo son p=1, p=2 o p=3 y, en lo que corresponde al modelo
de media móvil son q=1 y q=2.
Determinación de los órdenes de P y Q
Los órdenes de los parámetros P y Q se
analizan en la parte estacional del modelo, por lo que las autocorrelaciones en
los retardos periódicos de la serie transformada Volumen Facturado Total de
Agua Potable con d=1 y D=1 al establecer la prueba de significancia de r12 se
rechaza la hipótesis nula de nulidad del parámetro, y los subsiguientes r24,
r36, r48 y r60 son nulos estadísticamente. Esto permite determinar en forma
previa que el modelo a ajustarse podría tratarse de un modelo de media móvil de
orden 1 (Q=1).
Figura 5
Correlograma de
60 Autocorrelaciones parciales del Volumen Facturado Total de Agua
Potable con d=1
El tc=-5,04 rechaza la hipótesis nula
y el valor de r12 es significativo.
Al analizar las autocorrelaciones
parciales en los retardos periódicos de la serie transformada se aprecia que la
r12 es significativa y las restantes r24, r36, r48 y r60 no lo son, sugiriendo
que el modelo en la parte periódica es un autorregresivo de orden 1 (P=1).
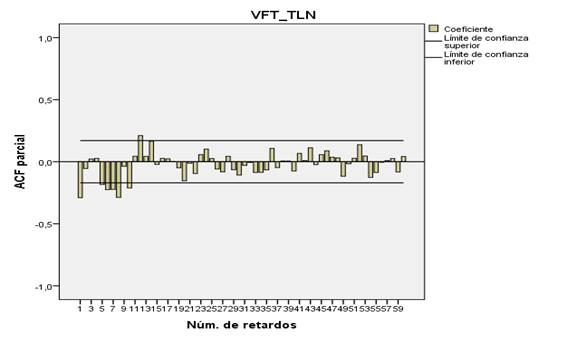
El correlograma de las
autocorrelaciones parciales en los retardos periódicos mostrados en la figura 6
permite visualizar que r12 se encuentra fuera del intervalo de confianza,
indicador que esta autocorrelación es significativa. En cambio, las
autocorrelaciones r24, r36, r48 y r60 se encuentran dentro de los intervalos de
confianza, indicando que no son significativos, por lo que el modelo a ajustar
es un autorregresivo de orden 1 (P=1).
Figura 6
Correlograma de
Autocorrelaciones parciales en los retardos periódicos del Volumen
Facturado Total de Agua Potable con d=1 y D=1
De lo analizado anteriormente se
deduce que P= 1 y/o Q= 1
Por tanto, el
modelo a ajustarse tiene los parámetros d=1, D=1, p=1, q=1, 2 ó 3, P=1 y Q=1,
no resultando claros los órdenes de la parte regular y estacional por la
imprecisión de la longitud de la estacionalidad en los períodos 11, 23, 36, 47
y 59 y no en los períodos 12, 24, 36, 48 y 60 como debiera ser en una serie con
estacionalidad mensual.
Ajuste del modelo
Bajo esa premisa se ajustaron combinaciones
de modelos según los órdenes determinados y que tienen los parámetros d=1, D=1,
p=1, q=1, 2 ó 3, P=1 y Q=1, sin descartar órdenes inferiores a los determinados
y que deben tomarse en cuenta en el ajuste del modelo óptimo
Desarrollo del
modelo ARIMA (0,1,1)(0,1,1)12 seleccionado incluyendo constante
El modelo ARIMA(0,1,1)(0,1,1)12 que
incluye la constante presenta los estadísticos como el R2 estacionario con un
valor de 0,55, es decir, que el modelo capta el 55% de la variabilidad total,
la raíz del error medio cuadrático (RMSE) de 0,038 que indica que varía en
±0.038 en promedio con respecto a los valores reales, el porcentaje medio del
error absoluto (MAPE) de 0,202 considerado como un porcentaje bajo de error. El
MAE de 0,028 es un valor que indica que los pronósticos no están sesgados dada
su cercanía al cero (0).
Tabla 2
Estadísticos del
modelo ARIMA (0,1,1)(0,1,1)12 con constante
|
Modelo |
Estadísticos de ajuste del modelo |
Ljung-Box Q(18) |
|||||
|
R2 estacionaria |
RMSE |
MAPE |
MAE |
Estadísticos |
GL |
Sig. |
|
|
VFT_TLN |
,550 |
,038 |
,202 |
,028 |
10,956 |
16 |
,812 |
En lo que concierne a los estimadores
del modelo, el parámetro MA con q=1 de la parte regular de la serie ![]() es significativo con p valor=0,000 de la
prueba t. Asimismo, el parámetro MA con Q=1 de la parte estacional
es significativo con p valor=0,000 de la
prueba t. Asimismo, el parámetro MA con Q=1 de la parte estacional ![]() es significativo con p valor=0,000, aun cuando
la constante resulta ser no significativa, lo cual es irrelevante.
es significativo con p valor=0,000, aun cuando
la constante resulta ser no significativa, lo cual es irrelevante.
Análisis de
residuos del modelo seleccionado. Prueba de Levene para varianza constante
La prueba de Levene para los residuos
del modelo que contrasta las hipótesis con p valor=0,390 basado en la media no
rechaza la hipótesis nula, y la varianza es constante en los errores. Al analizar
las treinta primeras autocorrelaciones de los errores del modelo ajustado se
aprecia que no son significativas, por tanto, puede afirmarse que tienen media
cero (0) y su correlación es cero (0).
Estos antecedentes permiten concluir
que los errores se comportan como ruido blanco con estadístico LJ-B=10.956 y
significancia p=0,812 se presentan en la tabla 2.
Tabla 3
Estimadores del
modelo ARIMA (0,1,1)(0,1,1)12 con constante
|
|
Estimación |
ET |
t |
Sig. |
||
|
|
Constante |
,000415 |
,000392 |
-1,057 |
,292 |
|
|
Diferencia |
1 |
|
|
|
||
|
MA |
Retardo 1 |
,590 |
,074 |
8,024 |
,000 |
|
|
Diferenciación estacional |
1 |
|
|
|
||
|
MA, estacional |
Retardo 1 |
,899 |
,175 |
5,152 |
,000 |
|
Con la serie hasta Marzo-2018, el
modelo ARIMA(0,1,1)(0,1,1)12 demuestra su consistencia al mantener los
pronósticos (variable codificada como VFTLN-est) el recorrido de los valores
observados (variable codificada como VFTLN), como se muestra en la figura 7:
Figura 7
Valores
observados y valores pronosticados en logaritmo natural
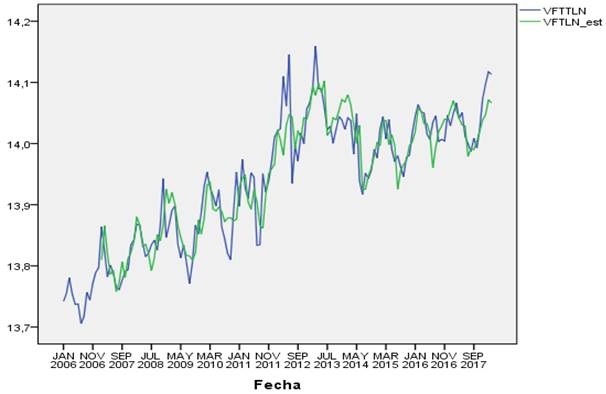
Valores
pronosticados y valores observados hasta 2018-marzo
Adicionalmente,
para el período entre agosto de 2017 a marzo de 2018, en el cual el modelo
ajusta adecuadamente, las métricas de error RMSE=0,0326 y MAE=0,0268 confirman
la consistencia del modelo. Finalmente, el modelo ARIMA (0,1,1) (0,1,1)
propuesto es:
![]()
Asimismo,
es posible determinar el componente tendencia del modelo de pronóstico de
series de tiempo en el consumo de agua potable en la ciudad de Tacna. La recta
propuesta por Gujarati y Porter (2010) indica que el coeficiente asociado a t
representa la pendiente de la serie que resulta significativa mediante la
prueba t. Por otro lado, la regresión resulta significativa mediante la prueba
F El resumen del reporte de SPSS 25 es el siguiente:
![]()
![]()
Fc: 315,010 p valor: 0,000
R2: 0,697 gle: 137
Se deduce que la pendiente de la recta
ajustada es significativa, y cuyo valor positivo indica que los consumos crecen
conforme se incrementa el tiempo.
Figura 9
Tacna:
Autocorrelaciones en los retardos periódicos del Volumen Facturado Total de
Agua Potable.
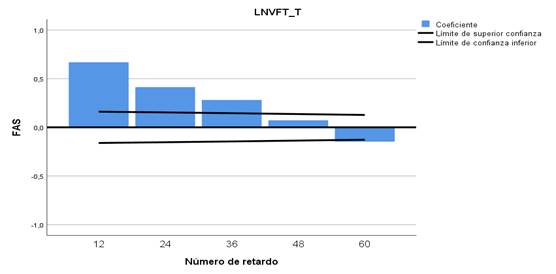
Asimismo, la estacionalidad es un componente
del modelo de pronóstico de series de tiempo en el consumo de agua potable en
la ciudad de Tacna, se demuestra al analizar los estadísticos t de los retardos
periódicos que proporcionan valores 8,36; 5,36; 1,14 y -2,33 son significativos
y la serie tiene estacionalidad de período 12.
El correlograma de las
autocorrelaciones en los retardos periódicos mostrado en la figura 9 y tabla 4,
corroboran la conclusión anterior, y dichas autocorrelaciones rebasan los límites
de confianza superior e inferior, excepto la autocorrelación en el período 48.
Tabla
4
Autocorrelaciones
en los retardos periódicos del Volumen Facturado Total de agua potable-Tacna.
|
Serie: LNVFT_T
|
||||||
|
Retardo |
Autocorrelación |
Desv. Errora |
Estadístico de Box-Ljung |
|
||
|
Valor |
gl |
Sig.b |
|
|||
|
12 |
,669 |
,080 |
937,261 |
12 |
,000 |
|
|
24 |
,413 |
,077 |
1367,994 |
24 |
,000 |
|
|
36 |
,282 |
,072 |
1534,196 |
36 |
,000 |
|
|
48 |
,072 |
,068 |
1588,344 |
48 |
,000 |
|
|
60 |
-,147 |
,063 |
1622,295 |
60 |
,000 |
|
Los
patrones cíclicos son fluctuaciones en forma de onda alrededor de la tendencia
y se aprecian en el largo plazo, sin embargo, en consonancia con Hanke y
Wichern (2010, p.167) “Es difícil tratar con el componente cíclico de una serie
de tiempo…”, precisamente, porque se aprecian en el largo plazo, a diferencia
del componente estacional que se aprecia dentro de un año. Por tanto, tanto su
magnitud como su duración, están lejos de ser constantes. Esta falta de un
patrón consistente de la onda hace que se dificulte la distinción entre los
ciclos y las tendencias que evolucionan con suavidad (Hanke y Wichern, 2010,
p.167).
Respecto
a los parámetros de calidad del agua potable que consume la población de Tacna
no se encuentran dentro de los rangos aceptables, se demuestra al analizar y
comparar los resultados de la Autoridad Nacional del Agua (2018), sobre los
resultados obtenidos en la Cuenca Maure indica que los parámetros de
conductividad, fósforo, arsénico, cadmio, mercurio y coliformes exceden lo
establecido en el Estándar de Calidad Ambiental para el Agua. Y, en la Cuenca
Caplina, los parámetros de pH, arsénico total, aluminio, hierro total, los
parámetros exceden el estándar ECA, debiendo remarcarse que los resultados se
refieren a las fuentes de agua a nivel de cuenca.
El
informe de la MCPLP (2017) establece que las fuentes para consumo humano en
Tacna son el Sistema Uchusuma y el Sistema Caplina y que desde el año 2003 la
Dirección Regional de Salud (DIRESA TACNA) realiza el estudio físico químico de
la calidad del agua para consumo humano concluyendo que el principal elemento
contaminante es el arsénico cuyo nivel se encuentra por encima del límite
máximo permisible (0,02 mg/l) y que las fuentes de agua se contaminan por medio
de un proceso natural, siendo necesario la búsqueda de otras fuentes de abastecimiento
o la implementación de tecnologías de remoción de este elemento, lo que permite
concluir esta hipótesis de que efectivamente, persisten algunos parámetros de
calidad del agua que están fuera de los rangos máximos permisibles, siendo el
más crítico el relacionado al arsénico. El modelo de pronóstico de series de
tiempo con variables de consumo rezagadas en el tiempo considerando patrones de
tendencia creciente y estacionalidad mensual aplicado al consumo de agua de uso
poblacional en la ciudad de Tacna basado en la metodología Box Jenkins es el
adecuado en el caso de Tacna, se prueba a través del modelo seleccionado para
Tacna que es el modelo ARIMA (0,1,1)(0,1,1)12 con intercepto y cuya formulación
matemática es:
![]()
DISCUSIÓN
Clavijo
(2013) utiliza variables de consumo, ingreso y número de habitantes; Olmeda
(2013) utiliza un modelo econométrico considerando como variable endógena el
crecimiento medio del PBI, variables exógenas como inversión, capital humano y
tasa de utilización del agua; y Henao y Córdova (2007) hace hincapié en los
factores sociales, demográficos y económicos. Lo común de esos modelos es que
buscan explicar el consumo del agua desde el punto de vista de la demanda
seleccionando las variables que explicarían ese consumo.
El presente estudio propone un modelo basado
exclusivamente en el consumo mediante series de tiempo de la variable consumo
de agua y que es el modelo ARIMA (0,1,1)(0,1,1)12 con intercepto, cuya
formulación matemática es: ![]()
Obtenido
utilizando la metodología Box-Jenkins tiene las características de un buen
modelo y coincide con el obtenido por Daza (2008) en su investigación Demanda
de agua en zonas urbanas de Andalucía utilizando modelos ARIMA y Redes
Neuronales Artificiales para la predicción de demanda de agua quien determinó
que el modelo ARIMA (0,1,1) x (0,1,1)12 es el que mejor describe la serie,
aunque una vez analizados sus residuos, observó algunos años atípicos como 1988,
1989, 1996 y 1997, derivado por el cambio del comportamiento de los
consumidores como efecto de la sequía sufrida, y algunos picos de consumo en
los meses de Julio y Septiembre, que pueden estar justificados por mayor
afluencia de la población y las altas temperaturas.
La
representación del consumo de agua relacionado a las series de tiempo por la
estacionalidad que presenta en el verano, Espinoza y Marco (2008) proponen
modelos ARIMA (p,d,q) (P,D,Q)s a series de demanda diaria de agua urbana y
sostienen que la selección de un modelo depende de factores como el horizonte
de predicción así como la disponibilidad de datos de la variable exógena y, el
modelo que obtienen presenta R2=0,88. Los parámetros estimados para el modelo
son θ1=0,409 correspondiente al MA(1), θ2=0,167 correspondiente al MA(2) y
Θ=0,874529 correspondiente al SMA(1) y que se trata de un modelo ARIMA
(0,0,2)(0,0,1)12.
En
ambos casos, el modelo ARIMA solo toma en cuenta la parte de media móvil, tanto
en la parte regular, como en la estacional. El R2 obtenido por Espinoza y Marco
(2008) es 0,79 el cual es considerado relativamente alto, en comparación con el
modelo obtenido en el presente estudio que es de 0,637 aparentemente inferior
al modelo anterior, pero, que no son comparables, pues, según Gujarati (2010),
los R2 solo son comparables cuando la variable dependiente sea la misma y, en
el presente caso, no lo son, por cuanto uno de ellos utiliza los datos en su
forma original y el segundo, el modelo obtenido en el presente estudio, lo utiliza
en forma logarítmica, y por otro lado, los datos corresponden a muestras
extraídas de poblaciones diferentes.
Por
otro lado, el análisis de la serie indica que hay 2 valores extremos y
corresponden a abril de 2012 (1342310 m3) y marzo de 2013 (1410306 m3) y que
los meses de verano (fines de diciembre, enero, febrero y marzo) son aquellos
en los cuales los consumidores, de acuerdo al estilo de vida, y, que coincide
con las temperaturas máximas mensuales, y en el caso de la serie la más alta en
el período de análisis corresponde a
24,015 °C del año 2012 (sin embargo, los años 2009 y 2013 también fueron años
calurosos), como la más alta temperatura máxima anual (SENAMHI, 2017), elevan
su consumo de agua.
El
análisis de la oferta del proyecto de EPS TACNA (2018) muestra que los valores
medios de los principales parámetros de calidad del agua potable en el proceso
de tratamiento de Planta Calana, indica que el de Arsénico en el agua cruda es
de 0,130 mg/l y, el agua potable que se entrega a la población es de 0,035
mg/l, cuyos registros se realizan en forma mensual, indicando que el período de
registro se realizó en enero a diciembre de 2009 (EPS TACNA, 2018). Este nivel
se encuentra entre dos (02) límites máximos permisibles: el que establece la
OMS de 0,010 mg/l y, el que establece la norma DIGESA de 0,05 mg/l.
CONCLUSIONES
Las conclusiones
a las que se llega en el presente estudio son:
El
modelo de pronóstico para el consumo de agua de uso poblacional en la ciudad de
Tacna es el modelo ARIMA (0,1,1)(0,1,1)12 con intercepto y cuya formulación
matemática empírica es:
![]()
Obtenido
utilizando la metodología Box-Jenkins, el cual tiene como variable explicatoria
el Logaritmo del consumo de agua con patrones de tendencia y estacionalidad y
cuyas variables endógenas son los errores rezagados un momento en el tiempo
correspondientes a la parte regular y estacional correspondiente a la parte
estacional.
El componente
Tendencia de la serie de Consumo de agua de uso poblacional en la ciudad de
Tacna está dado por la regresión,
![]()
![]()
Obtenido
por mínimos cuadrados ordinarios Gujarati y Porter (2010).
La
estacionalidad en la serie de tiempo en el consumo de agua potable en la ciudad
de Tacna es mensual, demostrado por el análisis de las autocorrelaciones
periódicas.
Además,
Los estadísticos t para cada uno de los retardos proporcionan valores 8,36;
5,36; 1,14 y -2,33 los cuales, comparados con el valor crítico de la distribución
al 5% de significancia permiten rechazar la hipótesis nula, por lo cual las
autocorrelaciones en los retardos periódicos son significativos y la serie
tiene estacionalidad de período 12, lo que se visualiza en la tabla 4.
La
serie de tiempo del consumo de agua de uso poblacional de Tacna no tiene un
patrón cíclico, ya que estos se visualizan en el largo plazo (entre 40 o 50
años y más) información que la EPS Tacna no dispone para ese período. Los
valores medios de los principales parámetros de calidad del agua potable en el
proceso de tratamiento de Planta Calana, indica que el de Arsénico en el agua
cruda es de 0,130 mg/l y, el agua potable que se entrega a la población es de
0,035 mg/l, cuyos registros se realizan en forma mensual, indicando que el
período de registro se realizó en enero a diciembre de 2009 (EPS TACNA, 2018).
De acuerdo a los estudios realizados, puede colegirse que existen dos (02)
límites máximos permisibles: el que establece la OMS de 0,010 mg/l y, el que
establece la norma DIGESA de 0,05 mg/l. En cualquiera de los dos casos, el agua
potable que se entrega a la población es de 0, 035 mg/l, valor que se encuentra
entre los límites máximos que establece la OMS y la DIGESA de Tacna.
REFERENCIAS
BIBLIOGRÁFICAS
EPS
TACNA (2012). Plan Maestro Optimizado 2013-2043.
Daza,
F. (2008). Demanda de agua en zonas urbanas en Andalucía (Tesis doctoral
Universidad de Córdova), Universidad de Córdova.
EPS
TACNA (2018). Estudio Factibilidad, instalación e implementación de la Nueva
Planta Calana. División de Estudios y Proyectos
Ferrán,
M. (1997). SPSS para Windows. Mc Graw Hill.
Gujarati,
D. y Porter, D. (2010). Econometría. Mc Graw Hill.
Hanke,
John y Wichern, Dean. (2010). Pronósticos en los negocios. Prentice Hall.
Hernandez
Sampieri, R., Fernández, C. y Baptista, L. (2014). Metodología de la
Investigación. Mc Graw Hill Education.
Instituto
Nacional de Estadística. (2010). Perú: Estimaciones y proyecciones de población
total y edades quinquenales según departamento, provincia y distrito, 2005-2015.
Boletín Especial N° 21. Dirección Técnica de Demografía e Indicadores Sociales.
Instituto
Nacional de Estadística e Informática (INEI) (2009). Perú: Estimaciones y
Proyecciones de Población por Departamento, Sexo y Grupos Quinquenales de Edad
1995-2025. Boletín de Análisis Demográfico Nº 37. http://lagransaladenoticias.com/2017/05/29/inicio-primera-etapa-de-proyecto-reduccion-de-perdidas-de-agua/
López-Espinoza,
Antonio, Ríos, Américo, Soto, Ma. Eugenia, Efectos de la privación de agua en
un Programa de Reforzamiento sobre el peso corporal. El consumo de agua y
alimento en ratas. Acta Comportamentalia: Revista Latina de Análisis de
Comportamiento [en linea] 2004, 12 (diciembre). Disponible en: http://www.redalyc.org/articulo.oa?id=274525894004> ISSN
0188-8145
Mendez,
F. y Feliciano, O. (2010). Propuesta de
un modelo socio económico de decisión de uso de aguas residuales tratadas en
sustitución de agua limpia para áreas verdes (Tesis maestría en Proyectos de
Inversión). Universidad Nacional de Ingeniería. Facultad de Ingeniería
Económica y Ciencias Sociales.
Mesa
de Concertación para la Lucha Contra la Pobreza (2017). Alerta: Situación de la
calidad de agua para consumo humano en la región Tacna-2017. Descargado de https://www.google.com/search?q=situacion+de+la+calidad+del+agua+tacna+2017&oq=situacion+de+la+calidad+del+agua+tacna+2017&aqs=chrome..69i57.12248j0j8&sourceid=chrome&ie=UTF-8
Olmeda,
J. (abril de 2006). El agua y su análisis desde la perspectiva económica: Una
aplicación para el crecimiento económico. VII Reunión de economía mundial,
Alicante, España.
ONU-AGUA.
(2015). Agua para un mundo sostenible. Datos y Cifras. Informe de las Naciones
Unidas sobre los recursos hídricos en el mundo 2015. Descargado de
http://www.unesco.org/fileadmin/MULTIMEDIA/HQ/SC/images/WWDR2015Facts_Figures_SPA_web.pdf
ONU-AGUA.
(2005). El agua fuente de vida 2005-2015. Departamento de Información Pública
de las Naciones Unidas.
http://www.un.org/waterforlifedecade/pdf/waterforlifebklt-s.pdf
Región
Tacna (2016). Diagnóstico de la calidad del agua de la Región Tacna. Gerencia
regional de Recursos Naturales y Gestión del Medio Ambiente. Tacna: Gobierno
Regional de Tacna.
Rosasco
O. (2006). Abastecimiento, contaminación
y problemática del agua en el Perú. Academia Nacional de Medicina. Simposio.
SERVICIO
NACIONAL DE METEOROLOGÍA E HIDROLOGÍA. (2017). Descargado de https://www.senamhi.gob.pe/?p=descarga-datos-hidrometeorologicos