Vol. 5, N° e724,
año 2023
Vol. 5, N° e724,
año 2023
ISSN – Online: 2708-3039
DOI:
https://doi.org/10.47796/ing.v5i0.724
![]()
Artículo
original
Estimación de demandas sísmicas usando diferentes patrones básicos de
distribución de carga en análisis estático no lineal
Estimation of seismic demands
using different basic load distribution patterns in nonlinear static analysis
José Miguel Vega Arana[1]
![]() https://orcid.org/0000-0002-6361-4902
https://orcid.org/0000-0002-6361-4902
Leonel Chahuares Paucar[2]
![]() https://orcid.org/0000-0002-9649-8450
https://orcid.org/0000-0002-9649-8450
Recibido: 21/12/2022
Aceptado: 12/01/2023
Publicado: 25/01/2023
Resumen
Las demandas sísmicas obtenidas del análisis estático no
lineal juegan un papel muy importante en la evaluación o diseño basados en
desempeño. Se ha demostrado que los patrones invariantes de distribución de
cargas más empleados en estos análisis no siempre son adecuados para
representar la acción sísmica en las estructuras cuando estas incursionan en el
rango inelástico. Este estudio apunta a realizar una comparación de las
demandas estructurales obtenidas de análisis estático no lineal (pushover) empleando diferentes patrones básicos de
distribución de carga con las obtenidas de rigurosos análisis no lineales
tiempo-historia, las cuales son establecidas como benchmark.
Se abarcaron cuatro intensidades sísmicas, así como dos alturas de estructura.
Se adoptó el desplazamiento promedio máximo del techo del último nivel obtenido
de los diferentes análisis no lineales tiempo-historia como desplazamiento
objetivo en los análisis pushover con cada patrón.
Los resultados demuestran la falta de precisión que tienen los patrones más
empleados para estimar adecuadamente las derivas de entrepiso de los últimos
niveles. Se encontró que es posible obtener mejores estimaciones únicamente
para los últimos niveles empleando dos patrones de distribución propuestos. Las
demandas obtenidas para las curvaturas de sección son aceptables considerando
que son cantidades de orden muy bajo.
Palabras clave: demandas
sísmicas; patrones de distribución de carga; análisis estático no lineal;
análisis pushover; análisis no lineal tiempo-historia.
Abstract
Seismic demands
obtained from nonlinear static analysis play an important role in
performance-based design or evaluation. It has been proved that the invariant
patterns of load distribution most used in this kind of analysis are not always
appropriate to represent the seismic action in structures when getting into the
inelastic range. This study aims to compare the structural demands obtained
from nonlinear static analysis using different basic patterns of load
distribution with those obtained from the rigorous nonlinear time-history
analyzes, which are considered as the benchmark. Four seismic intensities were
considered, as well as two structure heights. The maximum average displacement
of the top of the last level obtained from the different non-linear time-history
analyzes was adopted as the objective displacement in the pushover analyzes
with each pattern. The results show the lack of precision that the most used
load distribution patterns have in order to adequately estimate the interstory drift ratio of the higher stories. It was found
that it is possible to obtain better estimates solely for the highest stories
using two proposed distribution patterns. The demands obtained for the section
curvatures were acceptable considering that they are quantities of very low
order.
Keywords: seismic demands; patterns
of load distribution; nonlinear-static analysis; pushover analysis; nonlinear
time-history analysis.
1.
Introducción
El análisis estático no
lineal es el procedimiento más usado en la ingeniería estructural para el
estudio de estructuras en el rango inelástico, a pesar de tener algunas
limitaciones desde el punto de vista metodológico y del alcance y exactitud de
sus resultados (Mora et al., 2006). Su aplicación se ganó un lugar en los
principales procedimientos relacionados con el diseño basado en desempeño,
permitiendo conocer el comportamiento estructural desde un enfoque más cabal y
real. En la actualidad existen varios códigos y estándares los cuales brindan
los alcances necesarios para la aplicación de este procedimiento, tales como FEMA
356, ASCE/SEI 41-17, Eurocode 8, ATC 40, entre otros.
Los diferentes métodos que presentan los códigos para la aplicación del
análisis estático no lineal han sido bastante aceptados y aplicados en la
ingeniería práctica; no obstante, estudios demuestran que el uso de los
patrones de distribución invariantes de cargas propuestos por los códigos no
siempre son los adecuados para representar de manera eficaz los efectos de las
variantes características dinámicas durante la respuesta inelástica o la influencia
de modos de vibración superiores (Kalkan & Kunnath, 2004a; Chopra & Goel, 2002) la incertidumbre en la elección del patrón de
distribución de carga se convierte en una de las más importantes desventajas
del análisis estático no lineal debido a que, al existir tantos casos distintos
en la ingeniería, no hay un acuerdo general acerca de cuál es la mejor opción
para dicho patrón (Krawinkler & Seneviratna 1998; Tso & Moghadam, 1998). Un patrón de distribución de cargas
inadecuadas podría ocasionar que los resultados de demanda obtenidos del
análisis estén muy distantes de la demanda real a la cual estará sometida la
estructura. Esta falencia del análisis estático no lineal es aún más notoria a
medida que se analizan estructuras con periodo fundamental de vibración cada
vez más largo o, dicho de otra forma, estructuras de elevada altura (Faramarz & Mehdi, 2010).
En la literatura académica
se han hecho esfuerzos en estudiar este tema y a su vez buscar opciones
metodológicas para que la aplicación de los procedimientos pushover
sea mejor, teniendo en cuenta las falencias que tiene el procedimiento
tradicional. Chopra & Goel,
(2002) en el artículo; A modal pushover analysis procedure to estimate seismic demands for buildings proponen un
procedimiento basado en la teoría de dinámica de estructuras que retiene
simplicidad conceptual y atractividad computacional
de los procedimientos actuales que usan un patrón invariante de distribución
cargas. En la investigación se demuestra que es posible obtener resultados
aproximados de la respuesta no lineal dinámica de una estructura obtenida del
riguroso análisis de respuesta tiempo-historia aplicando el análisis modal
desacoplado de respuesta tiempo-historia (UMRHA), esta es la base para la
aplicación del análisis pushover modal (MPA) que
proponen.
En el artículo se propone
el uso de tres patrones invariantes de distribución de carga correspondientes a
la distribución de fuerzas de inercia de los tres primeros modos para llevar a
cabo tres análisis del tipo estático no lineal. Posterior a eso, mediante la
regla de combinación modal SRSS, se determina las demandas sísmicas totales de
la edificación. Para la validación de este procedimiento, se utilizó una
estructura 2D metálica de 9 niveles, cuyo sistema resistente a fuerzas
laterales está conformado por pórticos perimetrales resistentes a momento. Para
la comparación de resultados, se llevó a cabo el riguroso análisis de respuesta
tiempo-historia, cuyos resultados de demanda fueron escogidos como benchmark. Además, también realizaron un análisis modal
desacoplado de respuesta tiempo-historia no lineal y establecieron el
desplazamiento de techo máximo de la historia de desplazamientos de cada modo,
como el desplazamiento objetivo para cada análisis pushover.
Los resultados demostraron que el procedimiento MPA es lo suficientemente
preciso como para la aplicación práctica en evaluación y diseño de edificios,
sin embargo, se presentaron algunos errores considerables para estimar las
rotaciones de rótulas plásticas producidas en la estructura, por lo que esta
demanda debe ser estudiada con cuidado si se aplica este procedimiento. Dicha
falencia fue superada en otra investigación realizada por Reyes y Chopra años después.
Por otro lado, Amini & Poursha (2017)
proponen un procedimiento llamado The single-run multi-mode pushover (SMP) análisis, cuya formulación
tiene como objetivo considerar el efecto de modos de vibración mayores para la
estimación de la demanda sísmica de edificios de elevada altura. La principal
simplificación de este procedimiento es que solo es necesaria una corrida (single-run) utilizando un solo patrón de
distribución de cargas, el cual tiene en consideración los efectos de modos de
vibraciones mayores. Dicho patrón es computado mediante la adición algebraica
de los patrones correspondientes a los modos a considerar. Otra de las
características importantes de este procedimiento, es que, para la adición
algebraica de los patrones, se tiene en cuenta las características de la demanda
usando la pseudo aceleración espectral (o espectro de
diseño) así como también los ratios de masa efectiva de los modos, todo lo
anterior para incorporar un mayor sentido en la adición de los patrones. Para
propósito de comparación, se usó dos estructuras 2D metálicas de 15 y 20
niveles conformadas por pórticos especiales resistentes a momento. Los
resultados fueron comparados con otros métodos propuestos por la literatura y
principalmente con el análisis de respuesta tiempo-historia no lineal, el cual
fue establecido como benchmark para la determinación
de la precisión de los diferentes patrones de distribución de carga; es
importante mencionar que el análisis de respuesta tiempo-historia también se
utilizó para determinar el desplazamiento de techo objetivo para los análisis pushover. Los resultados demostraron que el procedimiento
SMP puede estimar con una buena exactitud las demandas sísmicas de edificios
altos.
Así mismo, Ahmed Najam et al. (2018) plantearon un procedimiento que resulta
de una simplificación del procedimiento original MPA. La formulación está
basada en las mismas asunciones dadas para el desarrollo del procedimiento
UMRHA, el cual postula que es posible obtener resultados razonablemente exactos
mediante la aplicación de un procedimiento muy parecido al análisis modal
clásico, a diferencia que este considera una relación fuerza-desplazamiento no
lineal. La esencia del procedimiento propuesto en la investigación, es la misma
que el planteamiento displacement modification
descrito en el ASCE/SEI, el cual afirma que se puede estimar el máximo
desplazamiento de techo de una estructura mediante la multiplicación del
desplazamiento elástico por factores de modificación. Los autores mencionan que
diferentes investigaciones concluyen que los modos de vibración llegan a
diferentes niveles de no-linealidad, afirmación que es la idea principal para
el desarrollo del SMPA. En pocas palabras, el procedimiento consiste en obtener
el desplazamiento de techo objetivo mediante el planteamiento displacement modification
para posteriormente llevar a cabo un análisis estático no lineal para cada modo
significante y finalmente obtener las demandas sísmicas empleando la regla de
combinación modal SRSS (Square Root of the Sum of the Squares). Los autores se apoyaron en algunas
investigaciones para determinar los factores de modificación para convertir el
valor pico de desplazamiento de techo elástico a inelástico y así tener el
desplazamiento de techo objetivo para cada modo de vibración. Los autores
usaron estructuras de 20, 33 y 44 niveles para estudiar la exactitud del método
propuesto. Al realizar las comparaciones respectivas con los procedimientos
UMRHA y NLRHA (análisis no lineal de historia de respuesta) los autores
concluyeron que el método propuesto en la investigación brinda resultados
razonablemente precisos tanto con respecto a los aportes modales como también a
nivel global (contribuciones modales combinadas).
Dado ese contexto, se
estudiaron las demandas sísmicas obtenidas de análisis estático no lineal,
empleando diferentes patrones básicos de distribución de carga para observar su
capacidad de brindar resultados adecuados a diferentes intensidades sísmicas y aplicadas
a estructuras de diferente altura. Se llevó a cabo análisis tiempo-historia no
lineal con la finalidad de establecer los resultados de dichos análisis como benchmark. Como resultado final, se tiene una detallada
comparación de las demandas estructurales sísmicas más importantes (derivas,
curvaturas) obtenidas de los diferentes análisis.
2.
Metodología
2.1. Estructuras
de estudio
Se emplearon dos estructuras metálicas regulares de 5
y 10 niveles. Ambas estructuras son propuestas con fines prácticos cumpliendo
los requisitos mínimos de la norma E.090, ANSI/AISC 341-10; la estructura de 5
niveles es considerada IMF (intermediate moment frames) y la de 10
niveles es considerada SMF (special moment frames) según la
clasificación del ANSI/AISC 341-10. Las estructuras son regulares en planta y
elevación. Las luces son de 4 m en las dos direcciones y las todas las alturas
de entre piso son de 3 m para ambas estructuras. El material de las estructuras
es acero estructural ASTM A36. La demanda sísmica empleada para el diseño fue
la especificada por la norma E030, considerando la costa peruana como ubicación
geográfica de ambas estructuras. (AISC 341, 2010; RNE, 2006, 2019)
Por tratarse de una estructura regular, el estudio se
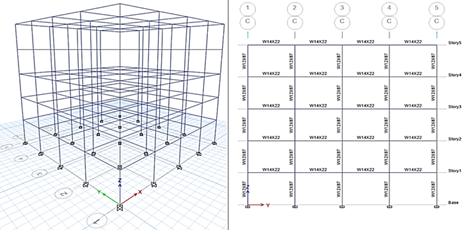
abocará al pórtico C de manera bidimensional. En la Figura 1 se muestra la
geometría, así como las secciones de los elementos de la estructura de 5
niveles y la Figura 2 de la estructura de 10 niveles.
|
Figura 1 Vista en 3D de estructura propuesta
(5 niveles) y vista en elevación del pórtico elegido (C) para el análisis de
las estructuras |
|
|
|
Nota. Elaborada y extraída de ETABS. |
|
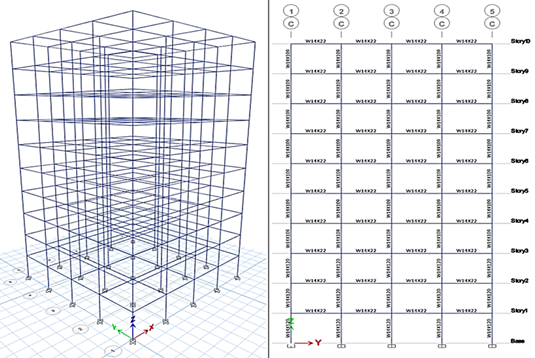
Figura 2 Vista en 3D de estructura propuesta (10 niveles)
y vista en elevación del pórtico elegido (C) para el análisis de las
estructuras |
|
|
|
Nota. Elaborada y extraída de ETABS. |
2.2. Patrones básicos de distribución de cargas
Se propusieron los siguientes patrones de distribución
de cargas dentro de los cuales se encuentran: el primer modo de vibración,
triangular, uniforme, doble triangular, triangular-uniforme, triangular a mitad
superior y parabólica a mitad superior. Son estos elementos los que harán la
diferencia entre los análisis de tipo estático no lineal. La propuesta de
dichos patrones apunta a cubrir una gama de patrones de distribución simples y
así verificar si alguno, con su respectiva simplicidad, estima adecuadamente
las demandas, respecto a las obtenidas por el análisis no lineal
tiempo-historia. En la Figura 3 se puede observar la forma de los patrones.
|
Figura 3 Patrones de distribución de carga |
|
|
2.3. Demanda
sísmica
La demanda sísmica establecida en este estudio se
representó considerando 4 eventos sísmicos en el territorio peruano; esto con
el fin de representar el ambiente tectónico de subducción que tiene la zona
oriente de Sudamérica. En cuanto a los registros sísmicos, se consideraron
ambas direcciones horizontales y se los escaló para alcanzar ciertos picos de
aceleración con el fin de manejar diferentes intensidades. Cabe resaltar que
estas intensidades son propuestas sin estar acordes a algún código.
Registros sísmicos empleados fueron: Ica 2007 (7 ML),
estación ICA002; Lima 2018 (5,1 ML), estación: ANCON; Piura 2021 (6,1 ML),
estación SCTRU; Tacna (6,9 ML), estación CREY.
Escalas propuestas: Leve (PGA = 0,2 g); Moderado (PGA
= 0,45 g); Severo (PGA = 0,7 g) y Crítico (PGA = 0,95 g).
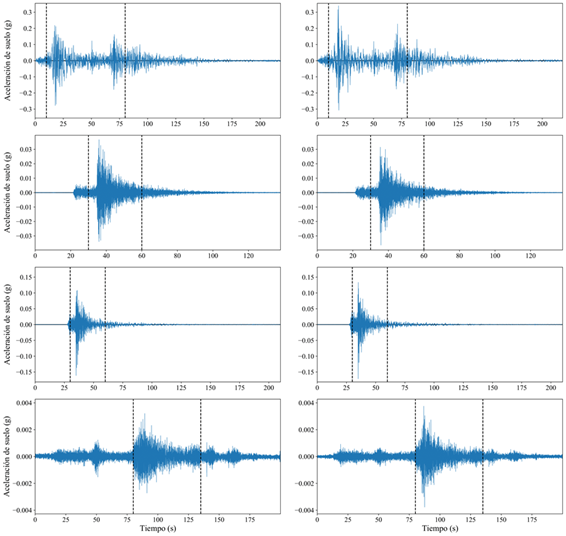
En la Figura 4 se puede observar los registros que se
emplearon para el estudio y los respectivos tramos considerados para eficiencia
del análisis.
|
Figura 4 Registros de aceleraciones de los sismos |
|
|
|
Nota. Registros de ambas direcciones horizontales; Ica 2007, Lima
2018, Piura 2021 y Tacna 2022 (de arriba hacia abajo). |
Con estos registros sísmicos se
pretende ver el comportamiento de las estructuras propuestas cuando incursionan
en el rango inelástico bajo acción sísmica de tipo subducción en Sudamérica.
2.4. Modelamiento
El modelamiento estructural y los
diferentes análisis fueron llevados a cabo en el software de código abierto OpenSees (Mckenna et al., 2010; Mazzoni et
al., 2006) el cual fue escogido por el alto potencial de cálculo que tiene en
el rango no lineal; es importante mencionar que este software es usado
alrededor del mundo para diferentes propósitos y, al ser un programa de código
abierto, tiene importantes y valiosos aportes de muchos investigadores
alrededor del mundo. Por preferencia se optó por usar el software en su versión
Py (Zhu et al., 2018) con
Python como lenguaje de programación interprete, por la gran ventaja que
presenta esta opción para presentación y visualización de resultados.
Se modeló las estructuras como
estructuras planas (2 dimensiones) dado que son totalmente regulares. La
geometría del modelo está basada en las dimensiones del centro-línea de los
elementos, es decir, el modelo solo contempla elementos línea que representen
las vigas y columnas de centro-línea a centro-línea. En cuanto a las uniones
entre elementos, se considera que es rígida, no permitiéndose desplazamientos
ni rotaciones relativas. Se consideró empotramiento perfecto en todos los
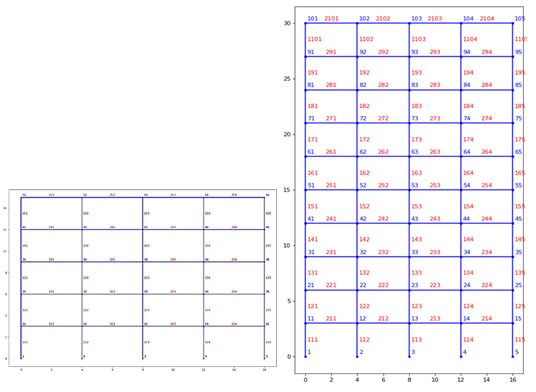
apoyos de la base. En la Figura 5 se puede observar el modelo de ambas
estructuras.
|
Figura 5 Modelos estructurales en dos dimensiones construidos
en OpenSees |
|
|
|
Nota. Estructura de 5 niveles
(izquierda), estructura de 10 niveles (derecha). Elaborada y extraída de OpenSeesPy. |
Como se observa en la Figura 5,
los únicos elementos que conforman el modelo estructural son las columnas y las
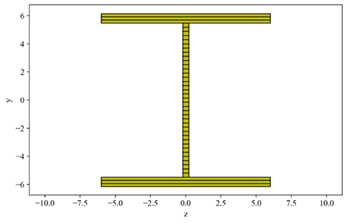
vigas, los cuales fueron modelados como elementos basados en fuerza (element_forceBeam Column) cuyo
comportamiento se rige por una sección de fibras (section_fiber),
tal como se observa en la Figura 6, capaz de capturar la interacción de carga
axial y flexión; las deformaciones por cortante son despreciadas por tratarse
de elementos bastante esbeltos. Además, esta formulación permite el
modelamiento de plasticidad distribuida en el elemento (Scott & Fenves, 2006), buscando el equilibrio de fuerzas y energía
a lo largo del elemento. Las hipótesis básicas más importantes son que las
secciones permanecen planas y que la deformación y esfuerzo es constante en
toda la fibra.
|
Figura 6 Sección de fibras para elementos basados en fuerza |
|
|
|
Nota. Fuente: Elaborada y extraída de OpenSeesPy. |
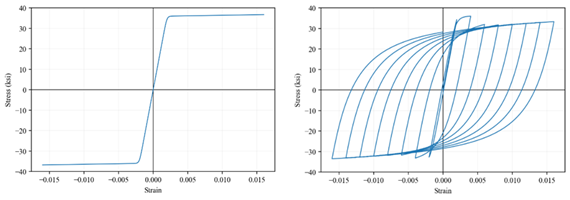
El material empleado para la
simulación fue el modelo Steel02 disponible
en OpenSees,
el cual considera un límite lineal y una zona plástica. El modelo también
captura los efectos de histéresis en el material, lo cual es muy importante en
análisis que presenten carga y descarga, como los análisis no-lineal
tiempo-historia. Esta es la ley constitutiva que gobierna la relación
esfuerzo-deformación de cada fibra de las secciones. La Figura 7 demuestra el
comportamiento del material empleado.
La masa sísmica considerada para
los análisis fue 4814,73 kgf s2m-1 para los niveles típicos y
4716,99 kgf s2m-1 para el
último nivel en el caso de la estructura de 5 niveles, mientras que para la
estructura de 10 niveles se consideró una masa de 4891,32 kgf
s2m-1 para los primeros 3 niveles, de 4865 kgf s2m-1 para los niveles 4 al 9, y
4742 kgf s2m-1 para el último
nivel.
Se definió la matriz de
amortiguamiento adoptando el modelo de Rayleigh con fracción de amortiguamiento crítico de 5 % para
el primer y tercer modo de vibración, valores que han sido empleados en
diferentes investigaciones (eg. Amini
& Poursha, 2017; Poursha
et al., 2009).
|
Figura 7 Modelo de acero estructural ASTM A36; comportamiento monotónico (izquierda), comportamiento histérico
(derecha) |
|
|
|
Nota. Elaborada y extraída de OpenSeesPy. |
Se consideró la no linealidad
geométrica proveniente del efecto P-Δ generado por el desplazamiento
transversal que experimentan las columnas. Esto se logró especificando dicha
formulación (geomTransf_PDelta) en todas las columnas
(Hajjar & Denavit,
2013). Con esto, se tiene un modelo capaz de capturar las dos fuentes más
comunes de no linealidad: no linealidad del material y la geométrica (Scott
& Jafari Azad, 2017).
2.5. Análisis no lineal tiempo-historia
Se llevó a cabo varios análisis
no lineales tiempo-historia empleando los registros ya indicados escalados a
las 4 intensidades sísmicas establecidas. Se obtuvieron los valores máximos de
las demandas sísmicas, tales como deriva de entre piso y curvatura de sección,
y las medias fueron definidas como benchmark para la
comparación final. También se determinó el desplazamiento de techo máximo para
cada caso, el cual fue establecido como desplazamiento objetivo para los
análisis pushover (ASCE/SEI, 2017) con los diferentes
patrones básicos de distribución de carga propuestos. Se llevaron a cabo dichos
análisis con las cargas gravitacionales ya aplicadas. Esto se realizó para
ambas estructuras.
2.6. Análisis estático no lineal
Se llevó a cabo un análisis
estático no lineal empleando cada patrón de distribución de carga presentado
empujando a la estructura hasta que el techo alcanza el desplazamiento objetivo
indicado en la sección anterior. Se determinan las derivas de entre piso y las
curvaturas de sección. Ambos procedimientos se realizan para todas las
intensidades previamente definidas. Al igual que en los análisis previos, se
hizo los análisis pushover con las cargas
gravitacionales aplicadas.
3.
Resultados
Se llevó a cabo todos los análisis respectivos y, como
se indicó previamente, la media de los resultados de los análisis no lineal
tiempo-historia fueron definidos como benchmark y se
realizaron las comparaciones de las derivas de entre piso y de las curvaturas
de la columna central y de las vigas vecinas a esta. A continuación, se
muestran los resultados obtenidos de los diferentes análisis.
2.1. Resultados de la estructura de 5 niveles
Curva Pushover
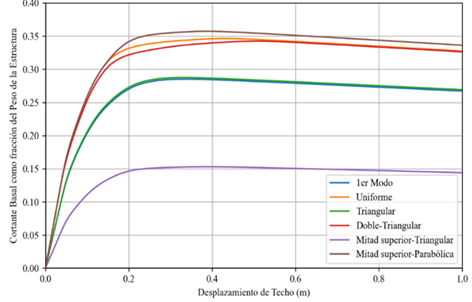
Se llevó a la estructura
hasta un desplazamiento de techo de 1 metro con los diferentes patrones de distribución
de carga. Como se observa en la Figura 8, así como algunos patrones brindan
resultados parecidos, existen también diferencias importantes en la fuerza que
requieren para deformar a la estructura de tal manera que el techo alcance un
desplazamiento determinado.
|
Figura 8 Curvas de capacidad para diferentes patrones de
distribución de carga para la estructura de 5 niveles |
|
|
Se llevó a la estructura
hasta un desplazamiento de techo de 1 metro con los diferentes patrones de
distribución de carga. Como se observa en la Figura 7, así como algunos
patrones brindan resultados parecidos, existen también diferencias importantes
en la fuerza que requieren para deformar a la estructura de tal manera que el
techo alcance un desplazamiento determinado.
Deriva de entre piso
Esta es quizás la demanda
más simple, pero valiosa, que brinda información de comprensión directa y de
fácil interpretación.
|
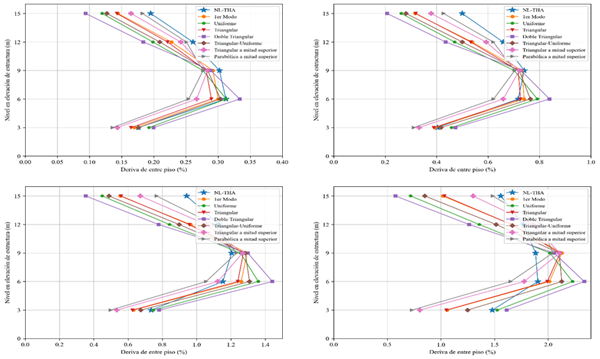
Figura 9 Derivas de entre piso |
|
|
|
Nota. Para intensidad leve
(superior-izquierda), moderada (superior-derecha), severa
(inferior-izquierda) y crítica (inferior-derecha) de la estructura de 5
niveles. |
|
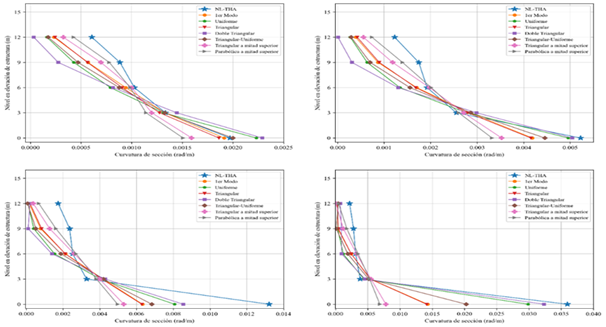
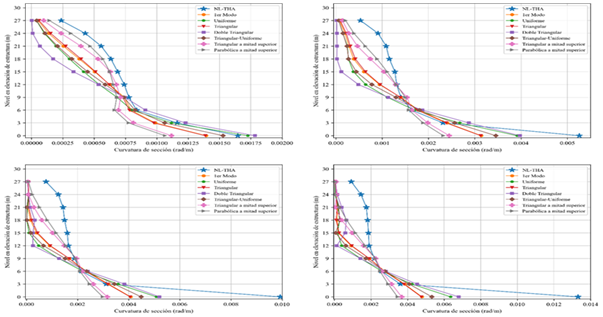
Figura 10 Curvatura de sección en la base de las columnas centrales |
|
|
|
Nota. Para intensidad leve (superior-izquierda), moderada
(superior-derecha), severa (inferior-izquierda) y crítica (inferior-derecha)
de la estructura de 5 niveles. |
De todos los análisis no
lineal tiempo-historia se determinó el desplazamiento de techo máximo promedio
para cada intensidad ya especificada, así como la deriva de entre piso máxima
promedio para cada nivel.
Para la comparación de las
derivas con los diferentes resultados del análisis pushover
se consideró las derivas de entre piso en el paso en el que el techo alcanzó el
desplazamiento de techo máximo promedio obtenido del análisis no lineal
tiempo-historia. En la Figura 9 se presentan los resultados.
Curvatura de Sección
Otra demanda sísmica de
interés en este estudio son las curvaturas. Para ello se presenta las
curvaturas de sección en la base de las columnas centrales y en la cara
viga-columna central de las vigas en todos los niveles. La Figura 10 muestra
las curvaturas de la base de las columnas centrales y en la Figura 11 las
curvaturas de vigas de cara a las columnas centrales.
|
Figura 11 Curvatura de sección en las vigas centrales |
|
|
|
Nota. Para intensidad leve
(superior-izquierda), moderada (superior-derecha), severa
(inferior-izquierda) y crítica (inferior-derecha) de la estructura de 5
niveles. |
2.2. Resultados de la estructura de 10 niveles
Curva Pushover
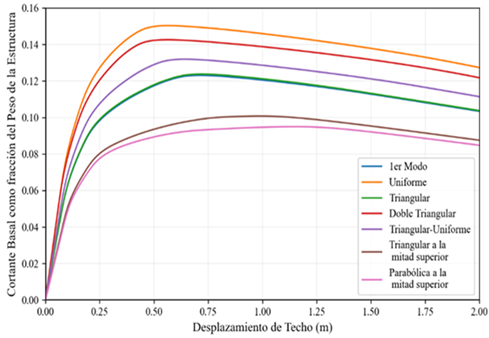
Se llevó a la estructura hasta
un desplazamiento de techo de 2 m. Al igual que la estructura anterior, en la
Figura 12 se puede apreciar cómo cambia la fuerza necesaria para empujar el
último techo para cada patrón de distribución de carga.
|
Figura 12 Curvas de capacidad para diferentes patrones de
distribución de carga para la estructura de 10 niveles |
|
|
Deriva de entre piso
Se presenta a continuación,
en la Figura 13, los resultados de deriva de entre piso obtenidos en los
análisis no lineales tiempo-historia y los obtenidos con cada patrón de
distribución.
Curvatura de sección
De igual manera se presenta
el resultado de la curvatura de sección para la base de la columna central en
la Figura 14 y de la viga central en la figura 15 para todos los patrones
empleados y el promedio de los resultados de los análisis no lineal tiempo-historia.
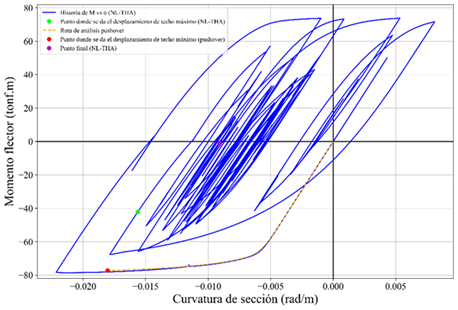
En cuanto a las curvaturas
de sección, los resultados no son útiles para comprender lo difícil que puede
ser reproducir un fenómeno de naturaleza dinámica mediante un análisis
estático. Se puede observar en la Figura 16 lo comentado en este párrafo.
|
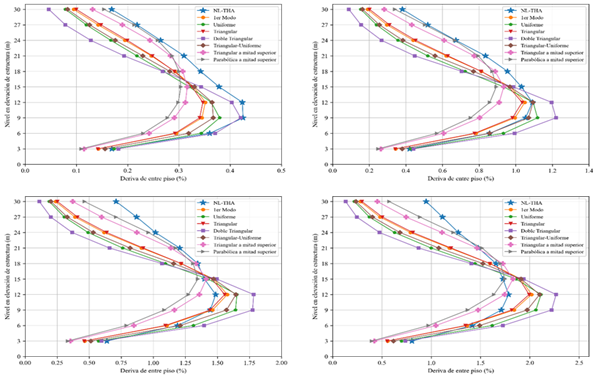
Figura 13 Derivas de entre piso |
|
|
|
Nota. Para intensidad leve (superior-izquierda),
moderada (superior-derecha), severa (inferior-izquierda) y crítica
(inferior-derecha) de la estructura de 10 niveles. |
|
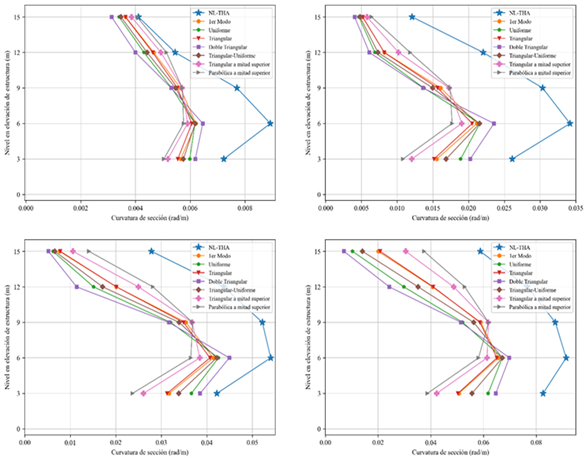
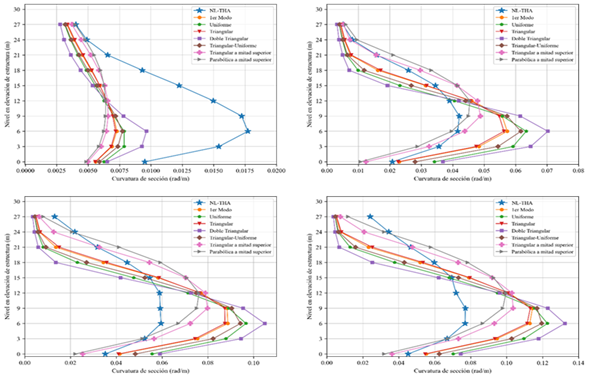
Figura 14 Curvatura de sección en la base de las columnas centrales |
|
|
|
Nota. Para intensidad leve (superior-izquierda),
moderada (superior-derecha), severa (inferior-izquierda) y crítica
(inferior-derecha) de la estructura de 10 niveles. |
|
Figura 15 Curvatura de sección en las vigas centrales |
|
|
|
Nota. Para intensidad leve
(superior-derecha), moderada (superior-derecha), severa (inferior-izquierda)
y crítica (inferior-derecha) de la estructura de 10 niveles. |
|
Figura 16 Gráfica de Momento-Curvatura obtenido de
diferentes análisis empleando la señal Ica 2007 escalada a intensidad crítico
(PGA = 0,95 g) |
|
|
4.
Discusión
4.1 Estructura de 5 niveles
En cuanto a las derivas de entre piso obtenidas, se
observa, en la Figura 9, que los valores obtenidos por el análisis no lineal
tiempo-historia es alcanzado adecuadamente por los patrones primer Modo y
Triangular-Uniforme en los primeros 2 niveles en intensidades leve y moderada,
mientras que en los niveles superiores los resultados de análisis
tiempo-historia salen ligeramente mayor que los que brindan los patrones de
distribución en estas dos intensidades. Esto sucede debido a la predominancia
del primer modo de vibración, dado que la estructura no ha incursionado mucho
en el rango no lineal, permite obtener estimaciones aceptables para las derivas
empleando los patrones mencionados. Para las demás intensidades, las respuestas
son sobreestimadas en los primeros tres niveles y en los últimos niveles
subestimados; esto guarda relación con estudios previos (Ahmed Najam et al., 2018; Amini & Poursha, 2017), los cuales obtuvieron una tendencia similar
con los patrones tradicionales. También es importante mencionar que la sobre
estimación de las derivas en los primeros niveles se explica por la formación
de rótulas en dichos niveles, lo que genera desplazamientos grandes en el techo
del último nivel, concentrando deformaciones de entre piso en los primeros niveles.
El patrón con mejor estimación para los dos últimos niveles para intensidad
crítica fue el Triangular a mitad superior Parabólico a mitad superior.
Ahora bien, respecto a las curvaturas de sección, para
el caso de la columna central, se observa en la Figura 10 que las estimaciones
de los patrones son buenas, generalmente hablando; de todas maneras, se resalta
que se subestima un poco esta demanda en los últimos dos niveles. Algo
interesante de notar, es que esta demanda en el primer piso va alcanzando valores
notoriamente mayores que algunas de las demandas calculadas empleando análisis pushover. El error en porcentaje respecto a la respuesta
real es considerable, pero esto es porque las curvaturas alcanzan valores muy
aleatorios dependiendo de la señal sísmica a la que se someta la estructura,
tal como se explicó en la Figura 16. La falta de precisión de para estimar esta
demanda también se vio expuesta en la investigación hecha por (Chopra & Goel, 2002).
Por otro lado, en la Figura 11 se contempla que para
las curvaturas de las vigas centrales se tiene una subestimación en todos los
casos considerados. Ninguno de los patrones de distribución es capaz de superar
las demandas benchmark en ningún nivel y bajo ninguna
intensidad. Los mejores resultados son alcanzados por los patrones Triangular a
mitad superior y Parabólico a mitad superior en los dos últimos niveles de
intensidad leve. La falta de una precisión general en los patrones se explicó
en el párrafo anterior.
4.2. Estructura de 10 niveles
En lo obtenido respecto a las derivas de entre piso,
se observa en la Figura 13 que el patrón con demandas más próximas a las
obtenidas por el análisis tiempo-historia es el Doble Triangular para los 5
primeros niveles y los Parabólicos a mitad superior y Triangular a mitad
superior para los 5 últimos niveles bajo la intensidad Leve; el hecho de que el
patrón del primer modo de vibración no se mencione debe estar relacionado con
que en las estructuras altas la contribución de modos superiores se hace
presente. Para las demás intensidades, las derivas de los primeros 5 niveles
son mejor estimadas por los patrones Triangular, Uniforme, Uniforme, Triangular
y primer Modo de manera general. Conforme la intensidad va en aumento, los
patrones Parabólico a mitad superior y Triangular a mitad superior siguen
siendo los que mejores estimaciones de derivas en los últimos niveles brindan,
sin embargo, la precisión va disminuyendo subestimando las demandas; esto
sucede por el aumento en la participación de los modos superiores a la respuesta
de desplazamiento dado que ya existen rótulas en la estructura y las
propiedades dinámicas cambian; como indican otras investigaciones (Chopra & Goel, 2002; Jalilkhani et al., 2020), mientras más alta sea una
estructura, el efecto de la participación de modos superiores, incluso sin
incursionar mucho en el rango no lineal, es mayor. En ese sentido, numerosas
investigaciones han hecho esfuerzos en buscar introducir la participación de
modos superiores en los análisis pushover (Chopra & Goel, 2004; Jalilkhani et al., 2020; Kalkan
& Kunnath, 2004b; Shakeri
& Mohebbi, 2010; Sullivan et al., 2021); a
diferencia de los estudios anteriores, en la presente investigación es estudió
las demandas obtenidas con algunos patrones de distribución básicos propuestos
por los autores en búsqueda de hallazgos nuevos con una metodología no
complicada.
Por otro lado, en cuanto a las curvaturas de sección
de la columna central, se contempla en la Figura 14 que, al igual que en la
estructura de 5 niveles, se obtienen demandas buenas de manera general, pero
hay grandes diferencias en la curvatura en la base, con excepción de la
intensidad Leve.
Finalmente, de los resultados de las curvaturas de
sección de las vigas centrales mostrados en la Figura 15 se puede mencionar que,
de manera resaltante, todos los patrones subestiman en gran manera las
curvaturas en casi todos los niveles. Para las demás intensidades, todos los
patrones, con excepción del Triangular a mitad superior y del Parabólico a
mitad superior, sobreestiman esta demanda considerablemente en los 5 primeros
niveles; en el sexto nivel estos patrones alcanzan una mejor estimación. Para
el nivel séptimo en adelante, los patrones Triangular a mitad superior y
Parabólico a mitad superior son los que estiman mejor las curvaturas. Ya se
hizo más comentarios respecto a esta demanda en la sección de la estructura de
5 niveles.
Este estudio investigó opciones prácticas y sencillas
en cuanto a los patrones de distribución de carga y a su vez empleó modelos
numéricos capaces de representar el comportamiento no lineal de estructuras.
Algo que podría ser una ampliación al alcance es el modelamiento en tres
dimensiones, lo que cubriría de manera más compleja el fenómeno en estudio. Por
otro lado, de los patrones propuestos, se resalta que el Triangular a mitad
superior y Parabólico a mitad superior fueron los que obtuvieron mejores
estimaciones de derivas en los últimos niveles, por lo tanto, se podría seguir
estudiando dichos patrones o proponer parecidos. También se menciona que se
podría plantear alguna combinación entre las derivas obtenidas de diferentes
patrones.
5.
Conclusiones
Es posible obtener demandas sísmicas adecuadas empleando varios
patrones básicos de distribución de carga, teniendo en cuenta la precisión y la
aplicación de los mismos mostrada en este estudio. Se observó que bajo ciertas
intensidades hay algunos patrones de distribución de carga que permiten obtener
mejores estimaciones de las cantidades de demanda para ciertos niveles (e.g. niveles inferiores) que las cantidades obtenidas por
otros patrones. No obstante, esta situación se revierte para el otro grupo de
niveles (e.g. niveles superiores).
Las mayores diferencias se encuentran en la estimación de las
curvaturas de sección, sin embargo, teniendo en cuenta que estas cantidades
siempre tienen valores de orden muy pequeño y que siempre se maneja un margen
de seguridad, se puede considerar estas estimaciones como buenas
aproximaciones.
Lo más resaltante encontrado en el estudio es como los métodos más empleados
pueden brindar buenas aproximaciones o también muy malas dependiendo lo que se
esté analizando. No está mal optar por procedimientos simplificados que se
tiene a disposición para análisis y diseño siempre y cuando se mantenga una
visión crítica de lo que se realiza y obtiene de estos procedimientos.
6.
Referencias Bibliográficas
Ahmed
Najam, F., Warnitchai, P., Mehmood, T., & Irshad Qureshi, M. (2018). A
Simplified Modal Pushover Analysis Procedure based on Displacement Modification
Approach.
AISC
341. (2010). Seismic Provisions for Structural Steel Buildings.
Amini, M. A., &
Poursha, M. (2017). A Single-Run Multi-Mode Pushover
Analysis for Seismic Evaluation of Tall Buildings. 16th World Conference on
Earthquake Engineering, 16WCEE 2017.
ASCE/SEI.
(2017). Seismic Evaluation and Retrofit of Existing Buildings. American Society
of Civil Engineers. https://doi.org/10.1061/9780784414859
Chopra,
A. K., & Goel, R. K. (2002). A modal pushover analysis procedure for
estimating seismic demands for buildings. Earthquake Engineering and Structural
Dynamics, 31(3), 561–582. https://doi.org/10.1002/eqe.144
Chopra,
A. K., & Goel, R. K. (2004). A modal pushover analysis procedure to
estimate seismic demands for unsymmetric-plan buildings. Earthquake Engineering
and Structural Dynamics, 33(8), 903–927. https://doi.org/10.1002/eqe.380
Faramarz,
K., & Mehdi, K. (2010). Evaluation of Proposed Lateral Load Pattern for
Estimating Seismic Demands on RC-Tall Buildings with Shear Walls in Pushover
Analysis. Advances in Structural Engineering, Vol. 14, 1017–1029.
Hajjar,
J. F., & Denavit, M. D. (2013). Description of Geometric Nonlinearity for
Beam-Column Analysis in OpenSEES.
Jalilkhani,
M., Ghasemi, S. H., & Danesh, M. (2020). A multi-mode adaptive pushover
analysis procedure for estimating the seismic demands of RC moment-resisting
frames. Engineering Structures, 213.
https://doi.org/10.1016/j.engstruct.2020.110528
Kalkan,
E., & Kunnath, S. K. (2004a). Lateral load distribution in nonlinear static
procedures for seismic design. ASCE, Structures.
Kalkan,
E., & Kunnath, S. K. (2004b). Method of modal combinations for pushover
analysis of buildingS. 13th World Conference on Earthquake Engineering,
13(2713).
Krawinkler,
H., & Seneviratna, G. D. P. K. (1998). Pros and cons analysis of seismic
evaluation. In Engineering Structures (Vol. 20).
Mazzoni,
S., Mckenna, F., Scott, M. H., Fenves, G. L., & Iii, A. (2006). Open System
for Earthquake Engineering Simulation (OpenSees) OpenSees Command Language
Manual.
Mckenna,
F., Scott, M. H., & Fenves, G. L. (2010). Nonlinear Finite-Element Analysis
Software Architecture Using Object Composition. Journal of computing in civil
engineering, 95–107. https://doi.org/10.1061/ASCECP.1943-5487.0000002
Mora, M. A., Villalba,
J. D., & Maldonado, E. (2006). Deficiencias, limitaciones, ventajas y
desventajas de las metodologías de análisis sísmico no lineal. Revista
Ingenierías Universidad de Medellín, 5(9), 59–74.
Poursha, M.,
Khoshnoudian, F., & Moghadam, A. S. (2009). A
consecutive modal pushover procedure for estimating the seismic demands of tall
buildings. Engineering Structures, 31(2), 591–599.
https://doi.org/10.1016/j.engstruct.2008.10.009
RNE. (2006). Norma
Técnica E.090 Estructuras Metálicas. www.construccion.org
RNE. (2019). Norma
Técnica Peruana E.030 Diseño Sismorresistente.
https://cdn.www.gob.pe/uploads/document/file/299950/d289856_opt.pdf
Scott,
M. H., & Fenves, G. L. (2006). Plastic Hinge Integration Methods for
Force-Based Beam-Column Elements. Journal of Structural Engineering, 132,
244–252. https://doi.org/10.1061/ASCE0733-94452006132:2244
Scott,
M. H., & Jafari Azad, V. (2017). Response sensitivity of material and
geometric nonlinear force-based Timoshenko frame elements. International
Journal for Numerical Methods in Engineering, 111(5), 474–492.
https://doi.org/10.1002/nme.5479
Shakeri,
K., & Mohebbi, M. (2010). Optimal Combination for Modal Pushover Analysis
by Using Genetic Algorithm. World Academy of Science, Engineering and
TechnologyInternational Journal of Computer and Information Engineering, 4(1),
45–51.
Sullivan,
T. J., Saborio-Romano, D., O’Reilly, G. J., Welch, D. P., & Landi, L.
(2021). Simplified Pushover Analysis of Moment Resisting Frame Structures.
Journal of Earthquake Engineering, 25(4), 621–648. https://doi.org/10.1080/13632469.2018.1528911
Tso,
W. K., & Moghadam, A. S. (1998). Pushover procedure for seismic analysis of
buiIdings. Progress in Structural Engineering and Materials, 1(3), 337–344.
Zhu, M., McKenna, F.,
& Scott, M. H. (2018). OpenSeesPy: Python library for the OpenSees finite
element frame