Vol. 3, N° 2
Vol. 3, N° 2
Julio - diciembre del 2021
ISSN – Online: 2708-3039
DOI: https://doi.org/10.47796/ing.v3i2.527
![]()
Artículo
original
Aplicación de la
estrategia teórica-aplicativa conjunta para mejorar el aprendizaje del método
de los elementos finitos en alumnos de pre y posgrado
Application
of the joint theoretical-applicable strategy to improve the learning of the
finite elements method in undergraduate and postgraduate students
Jorge Enrique Álvarez Ruffrán[1]
![]() https://orcid.org/ 0000-0002-5321-8500
https://orcid.org/ 0000-0002-5321-8500
José Alberto Acero Martinez[2]
![]() https://orcid.org/ 0000-0003-4154-9510
https://orcid.org/ 0000-0003-4154-9510
Recibido:
25/09/2021
Aceptado:
01/10/2021
Publicado:
19/11/2021
Resumen
Predecir el comportamiento exacto de elementos ante solicitaciones
ha sido y sigue siendo materia de estudio en diversas ramas profesionales,
siendo en un largo transcurso de tiempo el método de los elementos finitos
(MEF) una alternativa de solución a dicha premisa. Sin embargo, en contraste a
su relevancia, dicha metodología presenta alguna falencia en su aprendizaje, lo
cual crea muchas veces una falsa complejidad de aplicación en estudiantes
dispuestos a comprender la metodología. Debido a la complejidad que presenta el
aprendizaje teórico-aplicativo del MEF, la presente investigación tiene como
objetivo brindar una estrategia de aprendizaje sencilla de comprender,
relacionando directamente la parte teórica y aplicativa del método. Se realizó
una investigación a diversas publicaciones de autores destacados en la
metodología, recopilando sus diversas formas de enseñanza. A partir de dicha
investigación se establecieron los posibles elementos que puedan dificultar el
aprendizaje del MEF en estudiantes pre-profesionales. Teniendo en cuentas las
dificultades, las bases del método y las herramientas para una relación
teórica-aplicativa conjunta, se estableció una estrategia de enseñanza sencilla
de comprender para el estudiante. Las pruebas aplicadas a la metodología
teórica-aplicativa conjunta demuestran una mayor aceptación de la misma en los
estudiantes, adicionalmente mostraron una mayor dificultad de aprendizaje en la
parte teórica en comparación a la aplicativa. El enfoque típicamente dado a la
enseñanza aplicativa del MEF muestra tener una complejidad y dificultad en su
comprensión, en contramedida a esto la estrategia de aprendizaje presentada
resulta ser una alternativa de solución con resultados positivos respecto a una
mayor comprensión para el estudiante.
Palabras clave: Aprendizaje; Elementos
Finitos; Metodologías; Programación, Teoría.
Abstract
Predicting
the exact behavior of elements under stress has been and continues to be a
matter of study in various professional branches, with the finite element
method (FEM) being an alternative solution to this premise over a long period
of time. However, in contrast to its relevance, this methodology presents some
flaws in its learning, which often creates a false complexity of application in
students willing to understand this methodology. Due to the complexity
presented by the theoretical-applicative learning of the MEF, the present
research aims to provide a learning strategy that is easy to understand,
directly relating the theoretical and applicative part of the method. An
investigation was carried out on various publications of prominent authors in the
methodology, compiling their various forms of teaching. From this research, the
possible elements that may hinder the learning of the MEF in pre-professional
students were established. Taking into account the difficulties, the bases of
the method and the tools for a joint theoretical-applicative relationship, a
teaching strategy that was easy for the student to understand was established.
The tests applied to the joint theoretical-applicative methodology show a
greater acceptance of it in the students, additionally they showed a greater
learning difficulty in the theoretical part compared to the applicative part.
The approach typically given to the application teaching of the MEF, shows to
have a complexity and difficulty in its understanding. In countermeasure to
this, the learning strategy presented turns out to be an alternative solution
with positive results regarding a greater understanding for the student.
Keywords: Learning; Finite Elements; Methodologies;
Programming; Theory.
1.
Introducción
El método de los elementos finitos (MEF)
es una herramienta que nos ayuda a comprender el comportamiento de sistemas
ante solicitaciones, siendo usada en diversas carreras profesionales desde hace
mucho tiempo atrás. El extenso desarrollo de la metodología dio nacimiento,
solamente en 2008, a más de 25,000 publicaciones relacionadas al tema (Oñate,
2009), teniendo la metodología un gran alcance por las características que
presenta en comparación de otros métodos numéricos como el método de
diferencias finitas, el método de volumen finito, etc. (Rao, 2019). Bajo lo
cual se puede entender su amplio estudio y la importancia profesional que
conlleva el MEF, sin embargo, a pesar de las numerosas investigaciones
realizadas, la metodología presenta comúnmente dificultades en su aprendizaje
básico en los estudiantes. Dicha dificultad es debida a diversos factores, en
los cuales resalta el enfoque de aprendizaje y la complejidad/extensión que
presenta la propia metodología especialmente en elementos heterogéneos (Farmaga,
Shmigelskyi, Spiewak, y Ciupinski, 2011).
La investigación busca encontrar una
alternativa de solución ante dicha problemática, realizando un estudio a las
dificultades que presenta el aprendizaje del MEF. Conociendo las bases de
dichas dificultades y las características fundamentales de la metodología, se
presenta una nueva estrategia/metodología de aprendizaje que mezcla
directamente la parte teórica con la aplicativa. A lo largo de la investigación
se detalla dicha estrategia, el grado de aceptación por parte de los
estudiantes, entre otras características.
Bases
del MEF
Para realizar un aprendizaje integro de
cualquier metodología se inicia conociendo sus fundamentos teóricos, posterior
a esto se procede a relacionar/incorporar dichos conocimientos en la aplicación
de la metodología. Este concepto es general y el método de los elementos
finitos no es excepción.
El aprendizaje de las bases teóricas del
MEF abarca diversos temas que conllevan varias formulaciones demostradas
comúnmente por docentes del curso o investigadores del tema. Respecto a esto
último se cuentan con diversas publicaciones de autores con relevancia en el
tema, como “Structural Analysis with the Finite Element Method” (Oñate, 2013),
“The finite element method: its basis and fundamentals” (Zienkiewicz, Taylor, y
Zhu, 2005), entre otros. Dichos autores abordan detalladamente la parte
teórica, expandiéndose de forma breve a diversos campos de aplicación. Por todo
lo anterior, se puede inferir que la parte teórica no presenta un gran problema
siempre y cuando se aplique una metodología de aprendizaje fundamentada (el
estudiante cuente con bases y comprenda la dirección de su aprendizaje).
La pregunta que surge al comprender el
contexto del aprendizaje teórico de la metodología es ¿Qué sucede con su
aprendizaje aplicativo?
La
complejidad en la aplicación del MEF
La aplicación propia del MEF comprende el
cálculo de diversas variables, las cuales varían en función del enfoque dado a
la propia metodología. El cálculo de dichas variables presenta un grado de
dificultad en acorde al sistema que se esté analizando, a manera de
ejemplificar dicha dificultad evaluemos casos de obtención de la matriz de
rigidez local/global del sistema (matriz calculada generalmente en la
aplicación del MEF). Los ejemplos mostrados se basaron en la publicación
“Análisis aplicativo del método de los elementos finitos en un campo
estático-lineal e introducción a la no linealidad” (Alvarez Ruffrán, 2019).
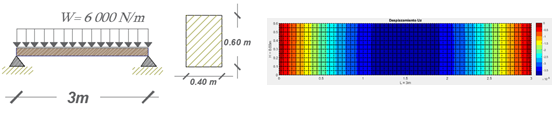
Es posible iniciar con casos sencillos
como son los sistemas unidimensionales, comúnmente enseñados en las primeras
etapas de aprendizaje. Dichos elementos se muestran en la figura 1 y pueden ser
abordados mediante cálculos manuales de una forma sencilla, mencionando que sus
matrices de rigidez global tienen dimensiones de 3x3 (a) y 8x8 (b), todo lo
anterior respecto a un caso de análisis sencillo.
|
Figura
1 Sistemas
unidimensionales sencillos |
|
|
Al pasar a realizar un análisis de mayor
nivel, tomaremos como ejemplo a los elementos bidimensionales. El caso de
análisis se muestra en la figura 2 y comprende un elemento tipo viga
simplemente apoyado, llegando a tomar su matriz de rigidez dimensiones de
4610x4610.
|
Figura
2 Sistema bidimensional – Viga simplemente
apoyada |
|
|
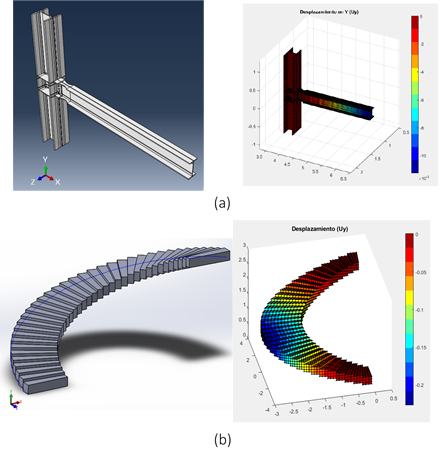
Pasando a elementos con mayor relevancia,
los cuales son objeto común de análisis en carreras de ingeniería civil y mecánica,
se puede dar como ejemplo una conexión de viga - columna empotrada, mostrada en
la Figura 3.a. La conexión mostrada desarrolla una matriz de rigidez global con
dimensiones de 61662x61662 bajo el análisis de un sistema tridimensional
sencillo.
Finalmente, se da como ejemplo un sistema
de escalera helicoidal (Figura 3.b). Dicho sistema es de análisis común para
diseños estructurales y comprende una matriz de rigidez global con dimensiones
de 18369x18369 elementos.
|
Figura
3 Ejemplos
de aplicación del MEF |
|
|
Teniendo en cuenta los casos analizados
se puede comprender el escalamiento en la dificultad que presenta el análisis
del MEF. Como se puede apreciar, únicamente los elementos unidimensionales son
los capaces de realizarse mediante cálculos manuales (siempre y cuando el
sistema sea sencillo). De igual manera, se debe tener en cuenta que tan solo se
ha hecho referencia a la obtención de la matriz de rigidez, el cual es uno de
uno de los diversos elementos necesarios para la aplicación la metodología.
Analizando todo lo anterior se puede
comprender en cierta medida que la metodología requiere necesariamente
herramientas de programación básica y en algunos casos medianamente avanzadas
para su correcta aplicación. Ante la necesidad de dichas bases de programación
surgen algunas problemáticas en su enseñanza para estudiantes universitarios de
carreras profesionales de ingeniería civil o mecánica, en donde la malla curricular
comúnmente no otorga dichas bases en su programación. Los estudiantes de
post-grado no comparten las mismas bases respecto al lenguaje de programación
con el que han trabajado. Todo esto crea una dificultad en la enseñanza por
parte del docente encargado del curso.
Cómo
es usualmente definida la aplicación del MEF
La metodología de elementos finitos
cuenta con diversos enfoques en función al público que se desea llegar, de esta
forma se han desarrollado publicaciones abarcando temas de estudio específico o
los propios fundamentos de la metodología. Con respecto a esto último, se
comprende el enfoque dado para el estudio general del MEF por autores con
relevancia en el medio.
La publicación titulada “The finite
element method for solid and structural mechanics” (Zienkiewicz y Taylor, 2005)
define el MEF en un caso lineal/no-lineal mediante diversos elementos y
demostrando detalladamente distintas formulaciones en la metodología. Con
respecto a la parte aplicativa, en el capítulo 19 se contempla netamente la
aplicación de la metodología mediante el anexo del software FEAPpv sin mostrar
en la propia publicación ejemplos de su uso.
Analizando la publicación “The finite
element method using MATLAB” (Bang y Kwon, 2000), los autores trabajan la
aplicación del MEF mediante la inserción de códigos los cuales son explicados y
ejemplificados a lo largo de su publicación. Sin embargo, el autor no se centra
en la parte teórica del método, brindando en gran medida expresiones
simplificadas a usar de forma directa y sistemática en los códigos.
En una publicación más antigua, pero de
mayor de mayor nivel crítico se evidencia la falencia en el aprendizaje
aplicativo del MEF; la publicación “An introduction to the finite element
method” (Reddy, 1993), en la cual se trata la aplicación de le metodología en
el Cap. 13 “Computer Implementation” brinda una serie de códigos difíciles de
entender desde el punto de vista de un estudiante pre-profesional (Figura 4).
Bajo estos casos de ejemplo y muchas
otras implementaciones de códigos enlistados en la publicación de Horst Werkle
(Werkle, 2008), se puede percibir que la aplicación del MEF se basa netamente
en la incorporación de códigos o programas en las diversas publicaciones, no se
genera ninguna relación directa entre la parte teórica y aplicativa. Dicho
enfoque de enseñanza dificulta el entendimiento aplicativo del método, ya que
el estudiante tendrá que dedicar gran parte del tiempo en comprender el
funcionamiento de dichos elementos en lugar de comprender el proceso de
aplicación de la metodología. Sin embargo, se debe resaltar que no se está
criticando las diversas publicaciones existentes, ya que están dirigidas a un
público general, centrándose específicamente en el desarrollo de la propia
metodología.
Teniendo en cuenta la dificultad en la
compresión de la aplicación del método por el enfoque dado, se puede inferir
que la dificultad en su aprendizaje surge cuando el estudiante opta por un
aprendizaje autodidacta sin ninguna guía respecto a las publicaciones óptimas
para su estudio. El estudiante tiene a las publicaciones como único medio de
referencia para la aplicación de la metodología. El docente del curso opta como
enfoque de enseñanza el abordado por las publicaciones mencionadas, esto
referido a la división en la forma desvinculada la enseñanza teórica y
aplicativa del método. Por ende, la currícula de la universidad opta por una
enseñanza enfocada en la parte teórica, aplicando en muy poca medida la
implementación del software estructural (Milton‐Benoit, Grosse, Poli, y Woolf,
1998). Todo esto crea un estereotipo de complejidad en el aprendizaje de la
metodología, por lo que tiende a ser difícil y tediosa.
|
Figura
4 Código
anexado |
|
|
Resolución
de un problema en programación
Se ha mostrado a lo largo de este
manuscrito la complejidad en cálculos que presenta la aplicación del MEF y, por
ende, el uso necesario de herramientas de programación. Con respecto a este
último se debe tener claro que la metodología es enseñada en carreras no
dedicadas netamente al campo de desarrollo del software (ingeniería
informática/sistemas), por lo que surge una dificultad en la
comprensión/elaboración de códigos por parte del estudiante. Dicha dificultad
no es tratada en las publicaciones mencionadas por el enfoque y el tipo de
público al cual están dirigidas. En el caso de un aprendizaje guiado por un
educador, la dificultad es comúnmente tratada como una sobrecarga en los
conceptos que el alumno debe conocer o estudiar a lo largo de todo el curso,
concentrándose en mayor medida en la comprensión de códigos que en el
desarrollo de la propia metodología, la cual es objetivo principal del curso.
La dificultad en la comprensión y
elaboración de códigos en estudiantes inexpertos no es un tema nuevo, siendo
abordada comúnmente en ciclos iniciales de las carreras de informática o
sistemas. Para facilitar la comprensión y elaboración de códigos en dichos
ciclos se introduce una metodología de desarrollo de aplicaciones, la cual se
agrupa de forma genérica en 3 fases o puntos (Joyanes Aguilar, 2003) mostrados
en la figura 5.
|
Figura
5 Resolución
de un problema en informática |
|
|
|
Nota. Adaptada de Joyanes Aguilar (2003). |
![]() El
primer punto de dicha metodología corresponde al estudio del problema,
entendiendo las bases que comprende el mismo. El según punto corresponde a la
elaboración de algoritmos que representa el procedimiento de solución del
problema a través del código/programa. El tercero y último punto corresponde a
la elaboración del código con base en lo trazado en el algoritmo.
El
primer punto de dicha metodología corresponde al estudio del problema,
entendiendo las bases que comprende el mismo. El según punto corresponde a la
elaboración de algoritmos que representa el procedimiento de solución del
problema a través del código/programa. El tercero y último punto corresponde a
la elaboración del código con base en lo trazado en el algoritmo.
Bajo el desarrollo de dicha metodología
se logra una compresión directa en estudiantes que aún no han interactuado
profundamente con códigos externos, dando solución a diversas problemáticas a
través de la relación directa de las bases y el proceso de solución del código.
El entendimiento del código sin interactuar con el tipo lenguaje de
programación trabajado (a través del algoritmo) genera una comprensión
intuitiva en el ingreso-tratamiento-exportación de data estipulado sin tener
que haberlo desarrollado.
La estrategia mencionada cumple los
requisitos de solución de la problemática presente en la comprensión aplicativa
del MEF, por tal motivo sirvió como base para el establecimiento de la
metodología conjunta enseñada en la presente investigación.
2.
Objetivo
El objetivo de la investigación es brindar una estrategia de
mejora en el aprendizaje del MEF, relacionando directamente la parte teórica
con la aplicativa.
3.
Metodología
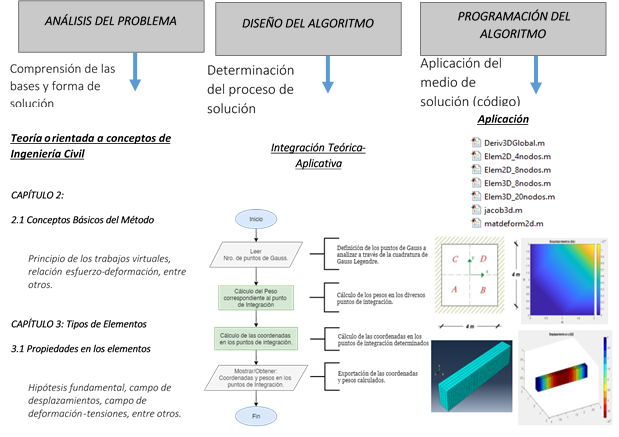
Para alcanzar el objetivo, se
adaptó la metodología de desarrollo de códigos en programación (Figura 5), ya
que sirve como medio de comprensión y aprendizaje de códigos en personas
inexpertas. En la Figura 6, se puede visualizar la adaptación de la metodología
para el proceso de aplicación del MEF, envolviendo los siguientes pasos:
(1) Bases del MEF. Conceptos fundamentales (Análisis del problema)
(2) Procedimiento de aplicación del MEF. Algoritmo (Diseño del
algoritmo)
(3) Aplicación sistemática del MEF. Código (Programación del algoritmo)
|
Figura 6 Desarrollo conjunto del MEF |
|
|
Bases del MEF
El planteamiento de los
conceptos fundamentales del MEF corresponde a las primeras etapas de
aprendizaje del método. Como se apreció anteriormente, dicha etapa no presenta
mayores dificultades en su comprensión, ya que existe un gran número de
publicaciones orientadas a la parte teórica, esto para un caso de estudio
autodidacta. En caso de seguir un aprendizaje guiado por un educador, se
recomienda orientar los fundamentos al estudiante desde un punto de vista
enfocado a la carrera profesional que se esté educando.
Procedimiento de aplicación del MEF
El procedimiento de aplicación
del MEF es el medio de integración entre la parte teórica y la aplicativa,
siendo básicamente la fase no considerada por muchos autores en el aprendizaje
de la metodología. Haciendo uso de algoritmos de programación en forma de
diagramas de flujo se puede ayudar visualmente al desarrollo del código en
programadores novatos (Hooshyar et al., 2015), comprendiendo de forma sencilla
la secuencia de aplicación y el desarrollo de diversos procesos desarrollados
en el método.
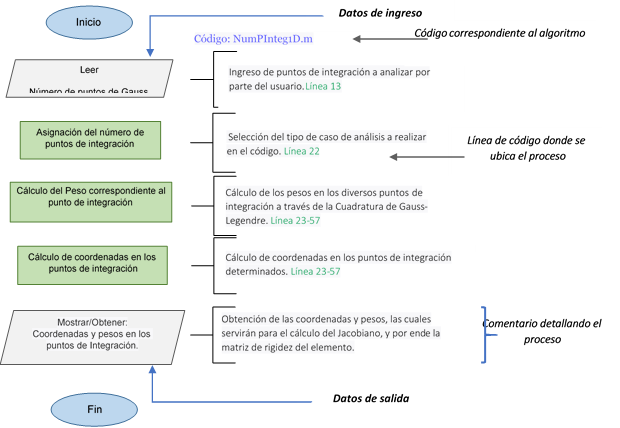
En la Figura 7, se muestra un
ejemplo de sub-proceso sencillo que corresponde a la obtención de coordenadas y
pesos en los puntos de integración, resaltando que mediante el algoritmo se
indican las respectivas líneas de códigos donde se realiza cada procedimiento,
el ingreso y salida de la data necesaria/resultante en el código correspondientes
al algoritmo trabajado, los comentarios donde se mencionan las bases teóricas
utilizadas para la ejecución de los diversos procesos y los bloques de decisión
que hacen énfasis a cuando se deberá realizar un procedimiento sistemático.
|
Figura 7 Algoritmo para sub-proceso sencillo |
|
|
Todas estas indicaciones
sirven como un medio de apoyo en favor de una comprensión más sencilla para el
estudiante, ya que podrá comprender el procedimiento de aplicación sin necesidad
de entrar a la propia programación.
Paralelamente se pueden
desarrollar otros algoritmos que especifiquen procesos más complejos o
generales como el que se visualiza en la Figura 8, en donde se muestra el
proceso general para la aplicación del MEF en barras. En dicho algoritmo se
incluye el bloque de toma de decisión, el cual será de gran ayuda para
especificar procesos sistemáticos.
|
Figura 8 Algoritmo para proceso general |
|
|
Aplicación del MEF
La incorporación de códigos
para la ejemplificación de diversos casos de análisis serán solamente un medio
para corroborar la correcta aplicación del MEF, debido a que el entendimiento
del proceso se basará en la comprensión de los algoritmos. De igual manera, la
comprensión de la estructura presente en los códigos podrá ser realizado mediante
los algoritmos.
Desarrollo de la integración
teórica-aplicativa
A lo largo de la publicación
se ha mostrado la dependencia de los algoritmos para una integración eficaz
entre la parte teórica y aplicativa (Figura 6), siendo estos el medio donde se
traza el proceso de aplicación para cada proceso o subproceso del MEF. Se debe
tener en claro que los algoritmos están basados netamente en los fundamentos
teóricos ya trabajados y trazan la forma que tendrán los distintos códigos de
aplicación.
Para demostrar la
representación de las distintas fases de un subproceso sencillo, se tomó como
ejemplo la obtención de la matriz constitutiva (elemento del MEF que representa
las propiedades del material – Figura 9) en la cual se aprecia que en primera
instancia se demostró y formuló la matriz, posteriormente se interpretó dicha
matriz como un subproceso en una etapa del algoritmo y finalmente se ejecutó el
proceso mediante su programación en el código correspondiente.
A través del ejemplo se
aprecia que los fundamentos teóricos sirven como base para la aplicación de la
metodología y son representados mediante procesos integrados en los algoritmos.
Los comentarios en los diversos bloques sirven para apoyar los fundamentos de
la metodología o mostrar el tipo de data de ingreso o salida en el proceso
|
Figura 9 Relación entre la teoría y aplicación |
|
|
Respecto a la realización de
los algoritmos para temas específicos, se recomienda seguir una secuencia de
ejecución para una integración completa entre ambas partes. La secuencia esta
mostrada en la figura 10, y se detalla a continuación:
1.
Comprensión de las bases teóricas necesarias
para realizar la aplicación de la metodología.
2.
Creación del algoritmo en función de las bases
teóricas y en forma de secuencia de procesos.
a. Incorporación de detalles en
el algoritmo mediante comentarios.
3.
Programación del código mediante el algoritmo
realizado.
4.
Verificación del código de ejecución e
incorporación de comentarios.
5.
Actualización del algoritmo en base a la
ubicación en líneas de código de los procesos.
|
Figura 10 Proceso de preparación de la estrategia |
|
|
Beneficios en la integración
teórica-aplicativa
La implementación de
algoritmos como medio de integración entre la teoría y aplicación del MEF
aporta diversos beneficios para una mejora en la comprensión por parte del
estudiante. En forma conjunta, también favorece al educador disminuyendo la
dificultad en la comprensión de los diversos temas a tratar. A continuación, se
enlistará algunos de los beneficios de mayor impacto en el uso de la estrategia
conjunta:
a Evitar el
aprendizaje/enseñanza de conceptos correspondientes al tipo de lenguaje de
programación a trabajar. Dicha omisión es debida a que el estudiante podrá
comprender el funcionamiento del código a partir del algoritmo, usando el tipo
del lenguaje que conozca para su representación.
a Comprensión directa de lo
detallado en los algoritmos al ser basados en los fundamentos teóricos
trabajados.
a Ubicación y comprensión
sencilla de los diversos procesos/subprocesos trabajados en los códigos
mediante el uso de los algoritmos y sus comentarios bajo los cuales estos se
relacionan.
Ensayo de la estrategia teórica-aplicativa
conjunta
Para probar la aceptación de
la estrategia por parte del estudiante, se desarrolló un ensayo que consistió
en simular una clase orientada al MEF bajo una estrategia de enseñanza “tradicional”
y otra con base en lo sustentado en esta investigación. La simulación se
realizó en una clase de pos-grado de ingeniería civil en la Pontificia
Universidad Católica del Perú, dicha clase está dedicada al estudio fundamental
del MEF. La cantidad de estudiantes que se sometieron a la simulación fueron
20.
En la simulación, se procedió
a dividir el salón en dos grupos mostrándoles una “clase” (simulación de clase,
ya que no se pretendía abarcarla en su totalidad) de aplicación del MEF bajo
dos estrategias de enseñanza distintas, posterior a esto los estudiantes
llenaron un formulario respondiendo preguntas específicas.
La primera estrategia simularía
una enseñanza tradicional con base en el enfoque de diversas publicaciones
mencionadas anteriormente. Se mostró al principio los fundamentos teóricos para
posteriormente desarrollar la parte aplicativa a través del uso de códigos, se
debe tener en cuenta que lo aplicado en los códigos se basó en lo desarrollado
en los fundamentos.
La segunda estrategia
simularía lo desarrollado en esta investigación. Inicialmente como el caso
anterior se inició enseñando la misma base teórica, posteriormente se
desarrolló la aplicación del MEF en forma secuencial, mediante los diagramas de
flujo. Finalmente, y solo como un acto complementario se enseñó el código de aplicación
enlazándolo directamente al diagrama ya trabajado.
Cabe resaltar que los dos
grupos recibieron una simulación bajo las mismas condiciones, respecto al mismo
tema a desarrollar, bases teóricas, resultado objetivo en la aplicación, una duración
de tiempo muy similar y una expresión de enseñanza neutral para ambos casos.
De esta forma no se benefició
a ninguna estrategia de enseñanza en particular.
4.
Resultados
El primer enfoque que se deseó
abordar fue respecto a la inclinación que percibieron durante la clase. La
respuesta de los estudiantes fue variada, siendo agrupada en dos enfoques
mostrados en la figura 11.
Es fácil notar la gran
diferencia en el enfoque que presenta la estrategia de aprendizaje mostrada en
esta investigación a comparación de la “tradicional”. Para el primer caso, se nota
que un 75 % de los estudiantes mostraron una asimilación de la información con
un mayor enfoque en la aplicación del MEF; en cambio para el segundo, la situación
prácticamente se invirtió con un 71 % de los estudiantes mostrando que el
enfoque planteado está más dirigido a comprender el código.
|
Figura 11 Enfoque de las metodologías |
|
|
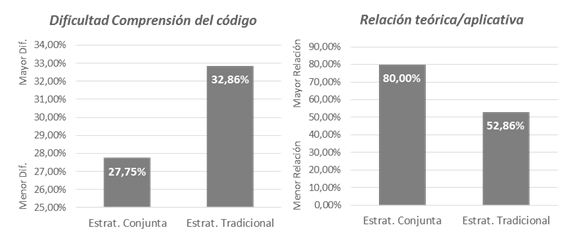
Simultáneamente se hizo el
estudio de la dificultad en la comprensión del código bajo las dos
metodologías, el cual se muestra en la primera gráfica de la figura 12. En
dicha gráfica se aprecia que los estudiantes perciben una menor dificultad en
la comprensión del código con la metodología presentada. Este resultado es de
gran relevancia ya que la presentación del código para la metodología conjunta
se aplica como una inclusión adicional para la comprobación de resultados. Lo
anterior se diferencia en gran medida a la estrategia tradicional dedicando
gran parte del tiempo en la comprensión/comprensión del código y aun así
presentando una mayor dificultad en el entendimiento por parte de los
estudiantes.
|
Figura 12 Dificultad del código – Relación
teórica/aplicativa |
|
|
Otro enfoque a comprobar en
los resultados fue la relación teórica/aplicativa percibida por los estudiantes
para ambas metodologías (Gráfica 2. Figura 12). En los resultados se muestra
que la estrategia conjunta relaciona en mayor medida la parte teórica con la
aplicativa. Este resultado demuestra el cumplimiento del enfoque abordado por
la estrategia desarrollada.
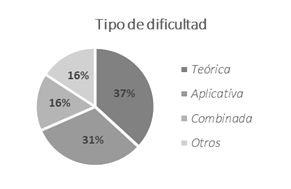
Finalmente, y de forma
adicional, se cuestionó a los estudiantes acerca de la mayor dificultad
presente en la compresión del MEF desde su punto de vista, se obtuvieron
resultados diversos, los cuales se pueden agrupar en categorías concretas
mostradas en la figura a continuación.
|
Figura 13 Dificultad del código –
Relación teórica/aplicativa |
|
|
5.
Conclusiones
La aplicación del MEF ha demostrado tener una
complejidad en su comprensión, esto debido no solo al tema de cálculos que lo
envuelven si no al enfoque con el que se aborda dicho tema. Como respuesta a la
problemática se presentó una estrategia conjunta de aprendizaje, involucrando
tanto la parte teórica como aplicativa, con resultados positivos en favor de
una mayor aceptación del estudiante. Dichos resultados concluyen que la estrategia implementada en esta investigación estimula más
y favorece a la comprensión de los estudiantes. De igual
manera, disminuye la dificultad en la comprensión del código para estudiantes
con diversos grados y tipos de conocimiento en lenguajes de programación
En caso de implementar la
metodología en cursos o publicaciones se especificaron los pasos a seguir para
una correcta aplicación, todo esto con base en una secuencia de procesos cuyo
fin es lograr la mayor correlación entre las bases teóricas y aplicativas del
MEF.
Adicionalmente, el estudio
realizado respecto a las dificultades que presenta el estudiante mostró una
mayor área de dificultad en la parte teórica, lo cual puede deberse a factores
como la metodología de enseñanza del docente. Para una mayor evaluación de esta
respuesta, se necesitaría un estudio más detallado que comprenda una mayor área de muestreo,
algo que se espera en un futuro.
Finalmente, con base en el estudio realizado
se comparte la premisa abordada en diversas publicaciones, respecto a la poca
importancia pre-profesional que se le otorga al aprendizaje de un método usado
profesionalmente en casi todo el software computacional de análisis
estructural/sólidos.
6.
Referencias Bibliográficas
Alvarez
Ruffrán, J. E. (2019). Análisis aplicativo del método de los elementos finitos
en un campo estático-lineal e introducción a la no linealidad.
Bang,
H., y Kwon, Y. W. (2000). The finite element method using MATLAB. CRC press.
Farmaga, I., Shmigelskyi, P., Spiewak,
P., y Ciupinski, L. (2011). Evaluation of computational complexity of finite
element analysis.
Hooshyar, D., Ahmad, R. B., Md Nasir,
M. H. N., Shamshirband, S., y Horng, S. J. (2015). Flowchart-based programming
environments for improving comprehension and problem-solving skill of novice
programmers: A survey. International
Journal of Advanced Intelligence Paradigms, 7(1), 24–56. https://doi.org/10.1504/IJAIP.2015.070343
Joyanes
Aguilar, L. (2003). Fundamentos de programación: algoritmos y estructura de
datos y objetos.
Milton‐Benoit, J., Grosse, I. R.,
Poli, C., y Woolf, B. P. (1998). The multimedia finite element modeling and
analysis tutor. Journal of Engineering
Education, 87(S5), 511–517.
Oñate, E. (2009). Structural Analysis with the Finite Element Method. Linear Statics.
https://doi.org/10.1007/978-1-4020-8733-2
Oñate, E. (2013). Structural analysis with the finite element method. Linear statics.
Springer Science y Business Media.
Rao, A. M. (2019). Applications of
finite elements method (FEM) -An Overview Abstract (December 2012). https://doi.org/10.13140/RG.2.2.36294.42565
Reddy, J. N. (1993). An introduction to the finite element method.
New York, 27.
Werkle, H. (2008). Finite Elemente in
der Baustatik: Statik und Dynamik der Stab-und Flächentragwerke.
Springer-Verlag.
Zienkiewicz, O. C., y Taylor, R. L.
(2005). The finite element method for
solid and structural mechanics. Elsevier.
Zienkiewicz, O. C., Taylor, R. L., y
Zhu, J. Z. (2005). The finite element
method: its basis and fundamentals. Elsevier.